Bài 1 trang 64 Toán 11 Tập 2 Chân trời sáng tạo

Bài 1 trang 64 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD.

a) Chứng minh CD ⊥ (SAD) .

b) Gọi M là trung điểm của AB . Chứng minh CM ⊥ (SAB) .

Giải bài 1 trang 64 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình vẽ sau: 

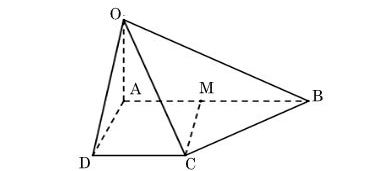
a) Chứng minh CD ⊥ (SAD)

Ta có:

SA ⊥ (ABCD) ⇒ SA ⊥ CD

Mà AD ⊥ CD

Suy ra: CD ⊥ (SAD) (đpcm)

b) Chứng minh CM ⊥ (SAB)

Ta có:

AB // CD ⇒ AM // CD

AM = CD = AB/2

⇒ AMCD là hình bình hành

Mà 

⇒ AMCD là hình chữ nhật.

Suy ra: CM ⊥ AB

Mà SA ⊥ (ABCD) nên SA ⊥ CM

Suy ra: CM ⊥ (SAB) (đpcm)