Bài 6 trang 74 Toán 11 Tập 2 Chân trời sáng tạo

Bài 6 trang 74 Toán 11 tập 2 Chân trời sáng tạo:

Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp.

Giải bài 6 trang 74 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

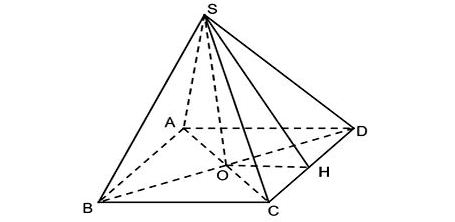
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều S.ABCD có O là tâm của đáy.

Kẻ SH ⊥ CD (H ∈ CD)

Ta có: SO = 21,6 m , AD = 34 m

Vì ΔSOC vuông tại O nên

Vậy độ dài cạnh bên bằng 32,3 m.

Xét ΔSCD cân tại S

⇒ SH vừa là trung tuyến, vừa là đường cao của ΔSCD

⇒ H là trung điểm của CD.

Mà O là trung điểm của AD.

⇒ OH là đường trung bình của tam giác ACD

⇒ OH = AD/2 = 34/2 = 17 (m)

Ta có: SO ⊥ (ABCD) SO ⊥ OH

⇒ ΔSOH vuông tại O.

Mà: 

Diện tích xung quanh của kim tự tháp là:

S_xq = 4.S_SCD = 4.467,5 ≈ 1870 (m²)

Vậy độ dài cạnh bênlà 32,3 m và diện tích xung quanh của kim tự tháp là 1870 m².