Bài 1 trang 73 Toán 11 Tập 2 Chân trời sáng tạo

Bài 1 trang 73 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với (ABC).

a) Chứng minh rằng (SBC) ⊥ (SAC).

b) Gọi I là trung điểm của SC. Chứng minh rằng (ABI) ⊥ (SAC).

Giải bài 1 trang 73 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình vẽ sau:

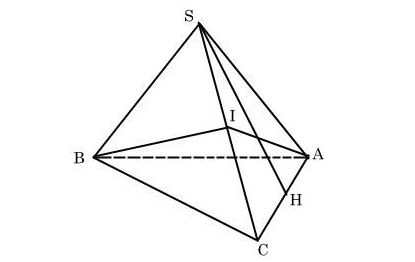
a) Gọi H là trung điểm của AC

Vì SAC là tam giác đều nên SH ⊥ AC 

Mà (SAC) ⊥ (ABC) 

⇒ SH ⊥ (ABC) ⇒ SH ⊥ BC  (1)

Lại có AC ⊥ BC (giả thiết)  (2)

Từ (1) và (2) suy ra: BC ⊥ (SAC)

Mà BC ⊂ (SBC) 

⇒ (SBC) ⊥ (SAC) (đpcm)

b) Vì tam giác SAC đều có I là trung điểm của SC nên AI ⊥ SC (1)

Lại có: BC ⊥ (SAC) nên BC ⊥ AI (AI ⊂ (SAC)) (2)

Từ (1) và (2) ⇒ AI ⊥ (SBC)

Mà AI ⊂ (ABI) nên (ABI) ⊥ (SAC) (đpcm)