Cách chứng minh 3 điểm thẳng hàng Toán lớp 8

Bài viết này trình bày chi tiết hướng dẫn cách chứng minh 3 điểm thẳng hàng Toán lớp 8, nhằm giúp các em học sinh ôn tập, vận dụng chứng minh 3 điểm thẳng hàng dễ dàng.

1. Cách chứng minh 3 điểm thẳng hàng lớp 8

Để chứng minh 3 điểm thẳng hàng Toán 8 ta vận dụng:

- Tính chất của hình bình hành: hai đường chéo cắt nhau tại trung điểm của mỗi đường.

- Nếu hai hình bình hành có một đường chéo chung thì hai đường chéo còn lại đi qua trung điểm của đường chéo chung đó.

2. Chứng minh 3 điểm thẳng hàng Toán 8 qua ví dụ

* Ví dụ 1: Cho hình sau, trong đó ABCD là hình bình hành. 

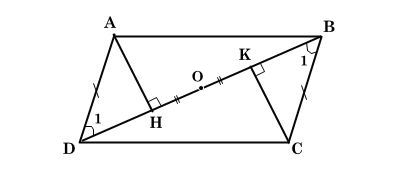
a) Chứng minh tứ giác AHCK là hình bình hành.

b) Gọi O là trung điểm của HK. Chứng minh ba điểm A, O, C thẳng hàng.

* Lời giải:

a) Ta có:

AH ⊥ BD (gt)

CK ⊥ BD (gt)

⇒ AH // CK (1)

Xét ΔADH và ΔCBK có:

AD = CB (cặp cạnh đối của là hình bình hành ABCD)

 (góc sole trong của AD // BC)

 (gt)

⇒ ΔADH = ΔCBK 

⇒ AH = CK

Từ (1) và (2) ta có tứ giác AHCK có hai cạnh đối song song và bằng nhau nên nó là hình bình hành. 

b) Áp dụng tính chất về đường chéo vào hình bình hành AHCK, ta được hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường.

Vì O là trung điểm của HK theo giả thiết nên AC đi qua O, hay A, O, C là ba điểm thẳng hàng. 

* Ví dụ 2: Cho hình bình hành ABCD. M, N lần lượt là trung điểm của hai cạnh AB và CD. E là trung điểm của MN. Chứng minh ba điểm B, E, D thẳng hàng.

* Lời giải:

Ta có hình vẽ sau: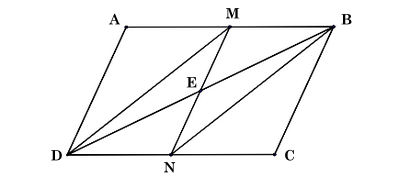

Ta có BM // ND và BM = ND nên BMDN là hình bình hành

Do đó, hai đường chéo MN và BD cắt nhau tại trung điểm của mỗi đường

⇒ E là trung điểm của BD

⇒ B, E, D thẳng hàng

3. Bài tập Chứng minh 3 điểm thẳng hàng Toán 8

* Bài tập 1: Một hình vuông ABCD có tâm O. Lấy điểm E thuộc AB thỏa mãn AE = AB/3. Từ D, kẻ đường thẳng vuông góc với đoạn OE, cắt CA tại M. Gọi N là giao điểm của OE với CD. Chứng minh ba điểm B, M, N thẳng hàng.

* Bài tập 2: Cho hình vuông ABCD. Lấy điểm M trên CB (MB > MC), điểm N trên AD (NA > ND) sao cho MB = NA. Gọi H là hình chiếu của M trên BN. Trên tia đối của MH lấy điểm K thỏa mãn EK = BN. Chứng minh ba điểm A, C, K thẳng hàng.

* Bài tập 3: Cho tam giác ABC thỏa mãn điều kiện: BC > CA > AB. Các điểm D, E, F lần lượt là chân các đường phân giác ứng với các đỉnh A, B, C của tam giác. Các điểm M, N, P, Q là các điểm mà đối xứng với B, A, C, A qua AD, BE, AD, CF. Trên CK lấy điểm I sao cho:  Chứng minh ba điểm M, N, I thẳng hàng.