Bài 12 trang 121 SGK Toán 8 tập 1 Cánh Diều
Cách giải Bài 12 trang 121 Toán 8 tập 1 Cánh diều - SGK đầy đủ dễ hiểu nhất
Bài 12 trang 121 Toán 8 Tập 1 Cánh Diều:
Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:
a) OD = (1/2)CM và tam giác ACM là tam giác vuông;
b) Ba điểm A, D, M thẳng hàng;
c) Tam giác DCM là tam giác cân.
Giải bài 12 trang 121 Toán 8 Tập 1 Cánh Diều:
Ta có hình vẽ sau: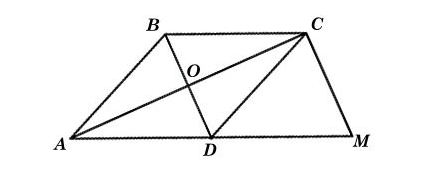
a) OD = (1/2)CM và tam giác ACM là tam giác vuông
• Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.
Vì BCMD là hình bình hành nên BD = CM.
• Ta có: CM // BD (do BCMD là hình bình hành)
AC ⊥ BD (chứng minh trên)
Do đó CM ⊥ AC hay
Vây ΔACM là tam giác vuông (đpcm)
b) Ba điểm A, D, M thẳng hàng
Vì BCMD là hình bình hành nên DM // BC
Do đó qua điểm D có hai đường thẳng AD và DM cùng song song với đường thẳng BC nên AD trùng với DM (Tiên đề Euclid)
Hay ba điểm A, D, M thẳng hàng.
c) Tam giác DCM là tam giác cân
Theo chứng minh ở câu a) thì BD // CM nên ta có:
(so le trong) (1)
(đồng vị) (2)
Do ABCD là hình thoi nên DB là tia phân giác của góc ADC
Do đó: (3)
Từ (1), (2) và (3) suy ra:
⇒ Xét ΔDCM là tam giác cân tại D (đpcm)
Trên đây KhoiA.Vn đã viết nội dung bài 12 trang 121 Toán 8 Cánh diều và hướng dẫn cách giải bài 12 trang 121 Toán 8 Cánh diều tập 1 SGK đầy đủ chính xác nhất. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết nhé, chúc các em thành công.
• Xem hướng dẫn giải Toán 8 Trang 120, 121 Cánh diều Tập 1
> Bài 7 trang 121 Toán 8 Tập 1 Cánh Diều: Cho tứ giác ABCD có ,
. Chứng minh ABCD là hình bình hành.
Đánh giá & nhận xét
- Bài 13 trang 121 SGK Toán 8 tập 1 Cánh Diều
- Bài 11 trang 121 SGK Toán 8 tập 1 Cánh Diều
- Bài 10 trang 121 SGK Toán 8 tập 1 Cánh Diều
- Bài 9 trang 121 SGK Toán 8 tập 1 Cánh Diều
- Bài 8 trang 121 SGK Toán 8 tập 1 Cánh Diều
- Bài 7 trang 121 SGK Toán 8 tập 1 Cánh Diều
- Bài 6 trang 120 SGK Toán 8 tập 1 Cánh Diều
- Bài 5 trang 120 SGK Toán 8 tập 1 Cánh Diều
- Bài 4 trang 120 SGK Toán 8 tập 1 Cánh Diều
- Bài 3 trang 120 SGK Toán 8 tập 1 Cánh Diều




































