Bài tập mở đầu về phương trình (PT một ẩn, PT tương đương) - Toán 8 bài 1 tập 2 chương 3

Bài viết này chúng ta sẽ áp dụng các kiến thức đó để giải một số bài tập liên quan trong bài mở đầu về phương trình.

• Lý thuyết phương trình một ẩn là gì? giải phương trình là làm gì? khi nào phương trình tương đương?

* Bài 1 trang 6 SGK Toán 8 tập 2: Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không:

a) 4x - 1 = 3x - 2

b) x + 1 = 2(x - 3)

c) 2(x + 1) + 3 = 2 - x

> Lời giải:

Thay giá trị x = -1 vào từng vế của phương trình, ta được:

a) Vế trái (VT) = 4x - 1 = 4(-1) - 1 = -5

Vế phải (VP) = 3x - 2 = 3(-1) - 2 = -5

VT = VP nên x = -1 là nghiệm của phương trình.

b) VT = x + 1 = -1 + 1 = 0

VP = 2(x - 3) = 2(-1 - 3) = -8

VT ≠ VP nên x = -1 không là nghiệm của phương trình.

c) VT = 2(x + 1) + 3 = 2( -1 + 1) + 3 = 3

VP = 2 - x = 2 - (-1) = 3

VT = VP nên x = -1 là nghiệm của phương trình.

* Bài 2 trang 6 SGK Toán 8 tập 2: Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)² = 3t + 4?

> Lời giải:

- Ta lần lượt thay các giá trị của t vào hai vế của phương trình ta được:

+ Với t = -1 :

 (t + 2)² = (-1 + 2)² = 1

 3t + 4 = 3(-1) + 4 = 1

⇒ t = -1 là nghiệm của phương trình (t + 2)² = 3t + 4.

+ Với t = 0

 (t + 2)² = (0 + 2)² = 4

 3t + 4 = 3.0 + 4 = 4

⇒ t = 0 là nghiệm của phương trình (t + 2)² = 3t + 4.

+ Với t = 1

(t + 2)² = (1 + 2)² = 9

3t + 4 = 3.1 + 4 = 7

⇒ t = 1 không là nghiệm của phương trình (t + 2)² = 3t + 4.

* Bài 3 trang 6 SGK Toán 8 tập 2: Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó.

> Lời giải:

- Vì phương trình nghiệm đúng với mọi x nên tập nghiệm của nó là S = R. (R tập số thực)

* Bài 4 trang 7 SGK Toán 8 tập 2: Nối mỗi phương trình sau với các nghiệm của nó (theo mẫu):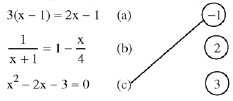> Lời giải:

+) Xét phương trình (a): 3(x – 1) = 2x – 1

Tại x = -1 có:

VT = 3(x – 1) = 3(-1 – 1) = -6;

VP = 2x – 1 = 2.(-1) – 1 = -3.

⇒ -6 ≠ -3 nên -1 không phải nghiệm của phương trình (a).

Tại x = 2 có:

VT = 3(x – 1) = 3.(2 – 1) = 3;

VP = 2x – 1 = 2.2 – 1 = 3

⇒ VT = VP = 3 nên 2 là nghiệm của phương trình (a).

Tại x = 3 có:

VT = 3(x – 1) = 3.(3 – 1) = 6;

VP = 2x – 1 = 2.3 – 1 = 5

⇒ 6 ≠ 5 nên 3 không phải nghiệm của phương trình (a).

+) Xét phương trình (b): 

Tại x = -1 biểu thức  không xác định

⇒ -1 không phải nghiệm của phương trình (b)

Tại x = 2 có:

VT ≠ VP nên 2 không phải nghiệm của phương trình (b).

Tại x = 3 có:

VT = VP nên 3 là nghiệm của phương trình (b).

+) Xét phương trình (c) : x² – 2x – 3 = 0

Tại x = -1 có: VT = x² – 2x – 3 = (-1)² – 2.(-1) – 3 = 0 = VP

⇒ x = -1 là nghiệm của phương trình x² – 2x – 3 = 0

Tại x = 2 có: x² – 2x – 3 = 2² – 2.2 – 3 = -3 ≠ 0.

⇒ x = 2 không phải nghiệm của phương trình x² – 2x – 3 = 0.

Tại x = 3 có: x² – 2x – 3 = 3² – 2.3 – 3 = 0

⇒ x = 3 là nghiệm của phương trình x² – 2x – 3 = 0.

Vậy ta có thể nối như sau: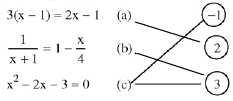

* Bài 5 trang 7 SGK Toán 8 tập 2: Hai phương trình x = 0 và x(x - 1) = 0 có tương đương không? Vì sao?