Công thức tính CHU VI, DIỆN TÍCH của một số hình trong thực tiễn? Toán 6 bài 3 Chân trời Tập 1 c3

Công thức tính CHU VI, DIỆN TÍCH của một số hình trong thực tiễn (hình vuông, hình chữ nhật, hình tam giác, hình thang, hình thoi, hình bình hành,...) ra sao? bài viết này sẽ cho các bạn lời giải đáp.

I. Chu vi và diện tích là gì

1. Chu vi là gì

Chu vi của một hình bất kì là độ dài phần đường thẳng bao quanh hình đó.

2. Diện tích là gì

Diện tích của một hình là toàn bộ phần bên trong của hình đó.

II. Công thức tính Chu vi và diện tích của hình vuông

Cho hình vuông có cạnh bằng a:

• Công thức tính Chu vi hình vuông là: C = 4a

• Công thức tính Diện tích hình vuông là: S = a.a = a²

* Ví dụ: Một mảnh ruộng hình vuông có cạnh bằng 20m. Năng suất lúa là 1,2kg/m². Tính diện tích mảnh ruộng và sản lượng thu hoạch được.

Diện tích mảnh ruộng hình vuông là: S = 20.20= 400 (m²)

Sản lượng thu hoạch được là: 400.1,2 = 480 (kg) 

III. Công thức tính Chu vi và diện tích của hình chữ nhật

Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là a, b:

• Công thức tính Chu vi hình chữ nhật là: C = 2(a + b)

• Công thức tính Diện tích hình chữ nhật là: S = a.b

* Chú ý: Khi tính chu vi và diện tích của các hình thì chiều dài và chiều rộng phải cùng đơn vị đo. Ký hiệu chu vi có thể là C hoặc P.

* Ví dụ: Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Loại gạch lát nền được sử dụng là gạch hình chữ nhật có chiều dài 20 cm, chiều rộng 50 cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?

* Lời giải:

Diện tích căn phòng hình chữ nhật là: S = 8.6 = 48 (m²)

Diện tích của một viên gạch là: 20.50 = 100(cm²) = 0,1(m²)

Số viên gạch bác Khôi cần dùng là: 48 : 0,1 = 480 (viên).

IV. Công thức tính Chu vi và diện tích của hình Thang

Cho hình Thang như sau:

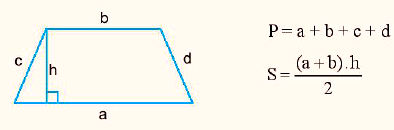- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó:

P = a + b + c + d

- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.

* Chú ý: Cách làm trên vẫn áp dụng được để tính chu vi và diện tích hình thang cân.

* Ví dụ: Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.

Diện tích hình thang cân là: 

V. Công thức tính Chu vi và diện tích Hình Tam giác

Cho hình Tam giác như sau: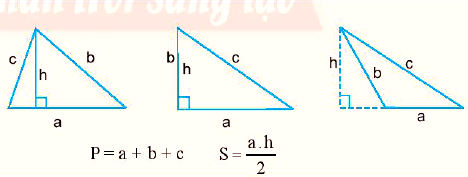

• Chu vi của hình Tam giác là: C = a + b + c (hoặc P = a + b + c)

• Diện tích của hình Tam giác là: 

VI. Công thức tính Chu vi và diện tích Hình Bình hành

Cho hình bình hành như sau:

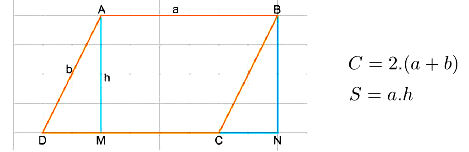
• Chu vi hình bình hành : C = 2(a + b)

• Diện tích hình bình hành là: S = a.h

Trong đó a là cạnh, h là chiều cao tương ứng.

VII. Công thức tính Chu vi và diện tích Hình Thoi

Cho hình Thoi hành như sau: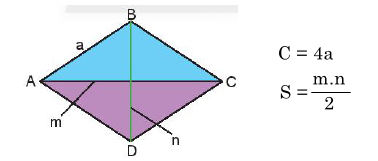

• Chu vi hình thoi bằng độ dài cạnh nhân với bốn: C = 4.a

• Diện tích hình thoi bằng nửa tích hai đường chéo: 

Trong đó a là cạnh, m và n là độ dài các đường chéo.

* Vi dụ: Hình thoi có độ dài hai đường chéo là 35 m và 25 m có diện tích là:

VIII. Chu vi và diện tích của một số hình trong thực tiễn

1. Tính chu vi của một số hình trong thực tiễn:

Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó

2. Tính diện tích của một số hình trong thực tiễn:

- Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi,…thì ta áp dụng công thức và tính.

- Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi,…

* Ví dụ: Cho một khu vườn với kích thước như hình 3a.

a) Tính chu vi khu vườn

b) Tính diện tích khu vường theo hai cách

- Tính diện tích hình ABCG và GDEF (hình 3b)

- Tính diện tích hình AHEF và BHDC (hình 3c)

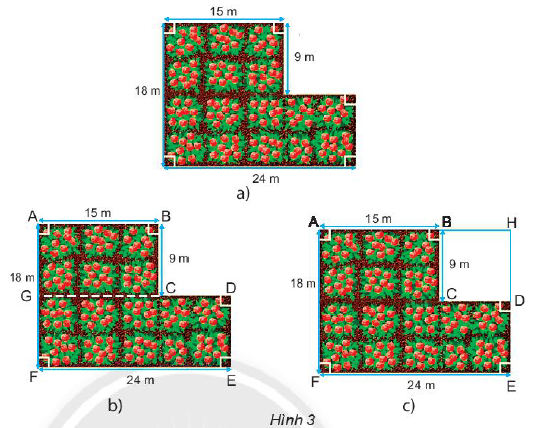* Lời giải:

a) Tính chu vi khu vườn

Ta có: CD = 24 - 15 = 9 (m)

DE = 18 - 9 = 9 (m)

Chu vi khu vường là:

P_{khu vườn} = AB + BC + CD + DE + EF + FA = 18 + 9 + 9 + 9 + 24 + 18 = 84 (m)

b) Tính diện tích khu vườn

- Tính diện tích hình ABCG và GDEF (hình 3b)

Ta có: FG = AF - AG = 18 - 9 = 9 (m)

S_{khu vườn} = S_ABCG + S_GDEF = AB.AC + EF.FG = 15.9 + 24.9 = 351 (m²)

- Tính diện tích hình AHEF và BHDC (hình 3c)

S_{khu vườn} = S_AHEF - S_BHCD = EF.FA - BC.CD = 24.18 - 9.9 = 351 (m²)