Bài 5 trang 106 SGK Toán 11 Tập 1 Chân trời sáng tạo

Bài 5 trang 106 SGK Toán 11 tập 1 Chân trời sáng tạo: Cho hình chóp S.ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng (ICD) cắt SA, SB lần lượt tại M, N.

a) Hãy nói cách xác định hai điểm M và N. Cho AB = a. Tính MN theo a

b) Trong mặt phẳng (CDMN), gọi K là giao điểm của CN và DM. Chứng minh SK//BC//AD

Giải bài 5 trang 106 SGK Toán 11 tập 1 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

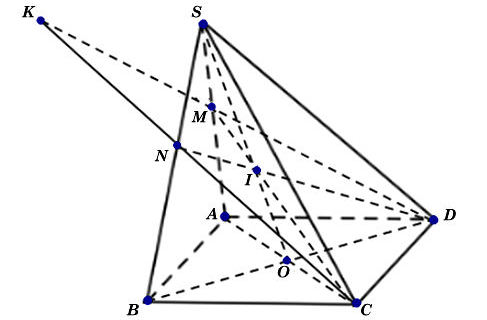
a) Trong mặt phẳng (SAC), gọi M là giao của CI và SA.

 CI ⊂ (ICD) nên M ∈ (ICD)

Trong mặt phẳng (SBD), gọi N là giao của DI và SB.

 DI ⊂ (ICD) ⇒ N ∈ (ICD)

Ta có MN là giao của của (ICD) và (SAB). Mà AB//CD nên MN//CD

Theo định lý Menelaus, trong tam giác SOA, ta có:

Ta có MN//AB nên 

b) Ta có:

 K ∈ CN mà CN ⊂ (SBC) ⇒ K ∈ (SBC)

 K ∈ DM mà DM ⊂ (SAD) ⇒ K ∈ (SAD)

Hơn nữa: S và K là hai điểm chung của hai mặt phẳng (SAD) và (SBC)

⇒ SK là giao tuyến của hai mặt phẳng (SAD) và (SBC).

Mà AD//BC ⇒ SK//BC//AD