Bài 4 trang 59 SGK Toán 10 tập 1 Cánh Diều

Bài 4 trang 59 Toán 10 Tập 1 Cánh Diều:

Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34.

Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.

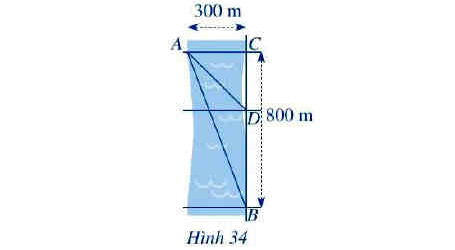
Giải bài 4 trang 59 Toán 10 Tập 1 Cánh Diều:

Ta có: 300 m = 0,3 km; 800 m = 0,8 km; 7,2 phút = 0,12 giờ. 

Gọi độ dài khoảng cách từ vị trí C đến D là x (km, x > 0).

Khi đó, ta có: AC = 0,3 km; CD = x km; BC = 0,8 km; DB = BC – CD = 0,8 – x (km). 

Mặt khác, ΔACD vuông tại C, áp dụng định lý Pythagore ta có: 

AD² = AC² + CD² = (0,3)² + x² = 0,09 + x² 

Vì vậy, khoảng cách từ vị trí A đến vị trí D là km, mà vận tốc chèo thuyền là 6 km/h và vận tốc dòng nước không đáng kể nên thời gian người đó chèo thuyền từ vị trí A đến vị trí D là:

  (giờ). 

Quãng đường từ vị trí D đến vị trí B là 0,8 – x (km) và vận tốc chạy bộ là 10 km/h nên thời gian người đó chạy bộ từ vị trí D đến vị trí B là:

 (giờ). 

Tổng thời gian người đó chèo thuyền là  t₁ + t₂ = t = 0,12 (giờ). 

 (*)

Bình phương cả hai vế của (*) ta được: 25.(0,09 + x²) = (3x + 1,2)² 

⇔ 2,25 + 25x² = 9x² + 7,2x + 1,44

⇔ 16x² – 7,2x + 0,81 = 0 

⇔ x = 0,225 (thỏa điều kiện x > 0)

⇒ x = 0,225 km = 225 m.

Vậy khoảng cách từ vị trí C đến D là 225 m.