Định lí Sin và định lí Côsin trong tam giác, giá trị lượng giác của một góc từ 0 đến 180? Toán 10 bài 1 c4cd1

Định lí Sin và định lí Côsin trong tam giác, giá trị lượng giác của một góc từ 0 đến 180⁰ như nào? bài viết này sẽ cho các bạn lời giải đáp.

I. Giá trị lượng giác của một góc từ 0° đến 180°

1. Định nghĩa giá trị lượng giác của một góc

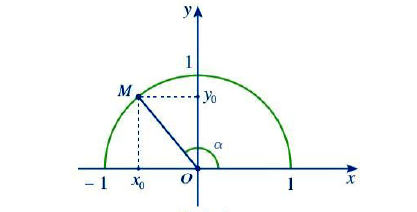Với mỗi góc α (0 ≤ α ≤ 180°) ta xác định một điểm M(x₀, y₀) trên nửa đường tròn đơn vị sao cho góc . Khi đó ta có định nghĩa:

• sin của góc α, kí hiệu là sinα, được xác định bởi: sinα = y₀;

• côsin của góc α, kí hiệu là cosα, được xác định bởi: cosα = x₀;

• tang của góc α, kí hiệu là tanα, được xác định bởi:  (x₀ ≠ 0);

• côtang của góc α, kí hiệu là cotα, được xác định bởi:  (y₀ ≠ 0).

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

* Chú ý:

sin(90° – α) = cosα (0° ≤ α ≤ 90°);

cos(90° – α) = sinα (0° ≤ α ≤ 90°);

tan(90° – α) = cotα (0° ≤ α ≤ 90°);

cot(90° – α) = tanα (0° ≤ α ≤ 90°).

2. Tính chất giá trị lượng giác của một góc

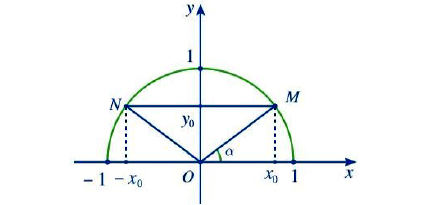
Trên hình bên ta có dây cung NM song song với trục Ox và nếu  thì . Với 0° ≤ α ≤ 180° thì:

sin(180° – α) = sinα,

cos(180° – α) = –cosα,

tan(180° – α) = –tanα (α ≠ 90°),

cot(180° – α) = –cotα (α ≠ 0°, α ≠ 180°).

* Ví dụ: Tính giá trị của biểu thức sau:

A = cos0° + cos20° + cos 40° + ... + cos160° + cos180°.

* Lời giải:

A = cos0° + cos20° + cos 40° + ... + cos160° + cos180°

= cos0° + cos180° + cos20° + cos160° + ... + cos80° + cos100°

= cos0° – cos0° + cos20° – cos20° + ... + cos80° – cos80°

= 0.

3. Bảng giá trị lượng giác của các góc đặc biệt

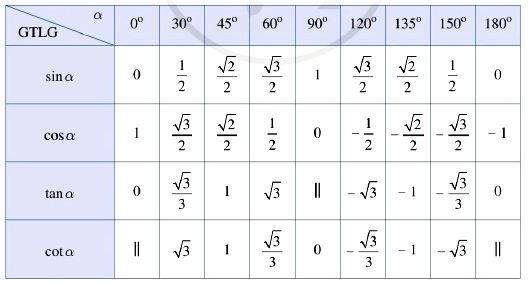
* Chú thích: Dấu “||” biểu thị sự không xác định của giá trị lượng giác tại góc đó.

* Ví dụ: 

* Chú ý: Cách sử dụng máy tính cầm tay để tính giá trị lượng giác:

- Ta có thể tìm giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng cách sử dụng các phím: sin, cos, tan trên máy tính cầm tay.

- Ta có thể tìm số đo (đúng hoặc gần đúng) của một góc từ 0° đến 180° khi biết giá trị lượng giác của góc đó bằng cách sử dụng các phím: SHIFT cùng với sin; cos; tan trên máy tính cầm tay.

II. Định lí Côsin

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:

a² = b² + c² – 2bccosA,

b² = c² + a² – 2cacosB,

c² = a² + b² – 2abcosC.

* Lưu ý:

* Ví dụ: Chứng minh a² = b² + c² – 2bccosA.

* Lời giải:

Cho tam giác ABC với BC = a, AC = b, AB = c, cosA = cosα

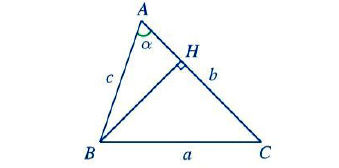
Kẻ BH vuông góc với AC.

Xét các tam giác vuông BHC và AHB, áp dụng định lý Py-ta-go ta có:

BC² = BH² + HC²

= BH² + (AC – AH)²

= BH² + AC² – 2.AC.AH + AH²

= (BH² + AH²) + AC² – 2.AC.AH

= AB² + AC² – 2.AC.AH

(BH² + AH² = AB² do áp dụng định lí Py-ta-go trong tam giác vuông AHB).

Xét tam giác vuông AHB, ta lại có: 

⇒ AH = AB.cosA = c.cosα

Do đó: a² = BC² = AB² + AC² – 2.AC.AH

= c² + b² – 2b. c.cosα

= b² + c² – 2bc.cosα (đpcm).

II. Định lí Sin

Cho tam giác ABC có BC = a, CA = b, AB = c và bán kính đường tròn ngoại tiếp là R. Khi đó:

* Lưu ý:

a = 2RsinA,

b = 2RsinB,

c = 2RsinC.

* Ví dụ: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60 m.

* Lời giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

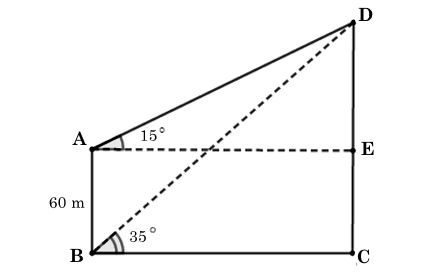Từ A hạ AE vuông góc với CD tại E.

Theo đề ra ta có: AB = 60m; 

Ta có: 

Mà  (tổng 3 góc của một tam giác bằng 180°)

Suy ra:

Áp dụng định lí sin trong tam giác ABD ta có:

Xét tam giác CBD vuông tại C, ta có:

CD = BD. = 169,45.sin35° ≈ 97,19 (m).

Vậy ngọn núi cao xấp xỉ 97,19 m.