Tổng và hiệu hai Vectơ, Quy tắc hình bình hành, hai vectơ đối nhau? Toán 10 bài 4 c4cd1

Tổng và hiệu hai Vectơ, Quy tắc hình bình hành, hai vectơ đối nhau như nào? bài viết này sẽ cho các bạn lời giải đáp.

I. Tổng của hai vectơ

1. Định nghĩa tổng của hai vectơ

Với ba điểm bất kì A, B, C, vectơ  được gọi là tổng của hai vectơ  kí hiệu là

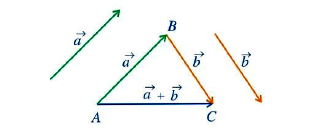
- Cho hai vectơ  và Lấy một điểm A tùy ý, vẽ  và . Vectơ  được gọi là tổng của hai vectơ  và . Ta kí hiệu tổng của hai vectơ  và là .

Vậy 

Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

2. Quy tắc hình bình hành

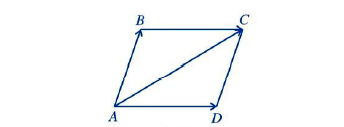
Nếu ABCD là hình bình hành thì 

* Ví dụ: Chứng minh quy tắc hình bình hành.

* Lời giải:

Ta có 

3. Tính chất phép cộng vectơ

Với ba vecto tùy ý  ta có:

- Tính chất giao hoán: 

- Tính chất kết hợp: 

- Tính chất của vecto-không: 

* Chú ý: Tổng ba vecto  được xác định theo một trong hai cách sau:

 hoặc 

II. Hiệu của hai vectơ

1. Hai vectơ đối nhau

Vectơ có cùng độ dài và ngược hướng với vectơ  được gọi là vectơ đối của vectơ , kí hiệu là . Hai vectơ  và  được gọi là hai vectơ đối nhau.

Quy ước: Vectơ đối của vectơ  là vectơ .

* Nhận xét:

• 

• Hai vecto ,  là hai vecto đối nhau khi và chỉ khi

• Với hai điểm A, B, ta có: 

* Lưu ý: Cho hai điểm A, B. Khi đó hai vectơ  và  là hai vectơ đối nhau, tức là 

* Chú ý: 

• I là trung điểm của đoạn thẳng AB khi và chỉ khi

• G là trọng tâm của tam giác ABC khi và chỉ khi

2. Hiêu của hai vectơ

Hiệu của hai vectơ  và ký hiệu  à tổng của vecto  và vecto đối của vecto , tức là 

Phép lấy hiệu của hai vecto được gọi là phép trừ hai vecto.

* Nhận xét: Với ba điểm bất kì A, B, O ta có: