Công thức HERON tính diện tích tam giác, cách tính cạnh và góc tam giác? Toán 10 bài 2 c4cd1

15:37:4310/11/2023

Lý thuyết bài 2, chương 4, SGK Toán 10 Cánh diều tập 1 về Công thức tính diện tích tam giác, Công thức HERON, cách tính cạnh và góc tam giác dựa vào điều kiện cho trước.

Công thức HERON tính diện tích tam giác, cách tính cạnh và góc tam giác dựa trên một số điều kiện cho trước như nào? bài viết này sẽ cho các bạn lời giải đáp.

1. Tính các cạnh và góc của tam giác dựa trên một số điều kiện cho trước

Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:

- Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;

- Biết độ dài ba cạnh;

- Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

* Ví dụ 1: Cho tam giác ABC có AB = 4, BC = 6, AC = $\small 2\sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB.

a) Tính cos các góc của tam giác ABC.

b) Tính độ dài cạnh AM.

* Lời giải:

Ta có hình vẽ sau:

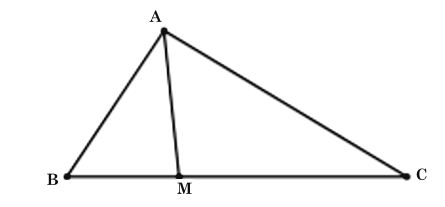
Tính góc và cạnh của tam giác

a) Tính cos các góc của ΔABC.

Theo định lí Cosin trong ΔABC ta có:

$\small cosB=\frac{AB^2+BC^2-AC^2}{2AB.BC}$ $\small =\frac{4^2+6^2-(2\sqrt{7})^2}{2.4.6}=\frac{1}{2}$

$\small \Rightarrow \widehat{B}=60^0$

$\small cosC=\frac{AC^2+BC^2-AB^2}{2AC.BC}$ $\small =\frac{(2\sqrt{7})^2+6^2-4^2}{2.2\sqrt{7}.6}=\frac{2\sqrt{7}}{7}$

$\small cosA=\frac{AB^2+AC^2-BC^2}{2AB.AC}$ $\small =\frac{4^2+(2\sqrt{7})^2-6}{2.4.2\sqrt{7}}=\frac{\sqrt{7}}{14}$

b) Tính độ dài cạnh AM.

Ta có:

$\small MC=2MB\Rightarrow \frac{MB}{MC}=\frac{1}{2}\Rightarrow \frac{MB}{BC}=\frac{1}{3}$

$\small \Rightarrow MB=\frac{1}{3}BC=\frac{1}{3}.6=2$

Áp dụng định lí cosin trong ΔAMB ta có:

AM² = AB² + BM² – 2AB.BM.cosB = 4² + 2² – 2.4.2. $\small \frac{1}{2}$ = 12

$\small \Rightarrow AM=\sqrt{12}=2\sqrt{3}$

* Ví dụ 2: Cho tam giác ABC có $\small \widehat{B}=35^0;\: \: \widehat{C}=50^0$ và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).

* Lời giải:

Ta có hình vẽ sau:

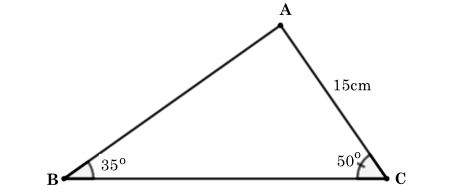
Tính góc và cạnh tam giác

Ta có: $\small \widehat{A}+\widehat{B}+\widehat{C}=180^0$ (tổng ba góc trong tam giác)

Suy ra: $\small \widehat{A}=180^0-(\widehat{B}+\widehat{C})$ $\small =180^0-(35^0+50^0)=95^0$

Áp dụng định lí sin trong ΔABC ta có:

$\small \frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AB}{sinC}$

$\small \Rightarrow BC=\frac{AC.sinA}{sinB}=\frac{15.sin95^0}{sin35^0}\approx 26,05(cm)$

$\small \Rightarrow AB=\frac{AC.sinC}{sinB}=\frac{15.sin50^0}{sin35^0}\approx 20,03(cm)$

Vậy BC = 26,05 cm và AB ≈ 20,03 cm.

2. Công thức Heron, công thức theo Sin để tính diện tích tam giác

• Công thức tính diện tích tam giác theo SIN

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

S = $\small \frac{1}{2}$ bc.sinA = $\small \frac{1}{2}$ ca.sinB = $\small \frac{1}{2}$ ab.sinC

* Ví dụ: Cho tam giác ABC có BC = $\small 4\sqrt{2}$ , $\small \widehat{A}$ = 45°, $\small \widehat{B}$ = 120°. Tính diện tích tam giác ABC.

* Lời giải:

Ta có: $\small \widehat{A}+\widehat{B}+\widehat{C}=180^0$ (tổng ba góc trong tam giác)

Suy ra: $\small \widehat{C}=180^0-(\widehat{A}+\widehat{B})$ = 180° – (45° + 120°) = 15°

Áp dụng định lí sin trong tam giác ABC ta có:

$\small \frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AB}{sinC}$

$\small \Rightarrow AC=\frac{BC.sinB}{sinA}=\frac{4\sqrt{2}.sin120^0}{sin45^0}=4\sqrt{3}$

$\small \Rightarrow AB=\frac{BC.sinC}{sinA}=\frac{4\sqrt{2}.sin15^0}{sin45^0}=2\sqrt{6}-2\sqrt{2}$

Diện tích tam giác ABC là:

$\small S=\frac{1}{2}AB.AC.sinA=\frac{1}{2}4\sqrt{3}(2\sqrt{6}-2\sqrt{2}).sin45^0$ $\small =12-4\sqrt{3}$ (đvdt)

• Công thức Heron tính diện tích tam giác:

Công thức Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $\small p=\frac{a+b+c}{2}$ .

Khi đó, diện tích S của tam giác ABC là:

$\small S=\sqrt{p(p-a)(p-b)(p-c)}$

Trong đó p là nửa chu vi tam giác ABC.

* Ví dụ: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.

* Lời giải:

Nửa chu vi tam giác ABC là:

$\small p=\frac{AB+AC+BC}{2}=\frac{5+6+9}{2}=10$

Áp dụng công thức Heron, diện tích tam giác ABC là:

$\small S=\sqrt{p(p-AB)(p-AC)(p-BC)}$ $\small =\sqrt{10(10-5)(10-6)(10-9)}=10\sqrt{2}$ (đvdt)

3. Áp dụng vào bài toán thực tiễn.

Trong thực tiễn, ta có thể áp dụng hệ thức lượng trong tam giác vào các bài toán như tính khoảng cách giữa hai vị trí, tính diện tích,... giúp cho việc tính toán trở nên chính xác và nhanh chóng hơn. Chúng ta có thể xem ví dụ sau:

* Ví dụ: Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

* Lời giải:

Giả sử toà nhà là AB, AB = 18,5 m; giác kế AC = 1,5 m; chiều cao của cái cây là DE; khoảng cách từ tòa nhà tới cây là BD = 30 m; góc tạo bởi phương quan sát gốc cây và phương nằm ngang là $\small \widehat{FCD}=34^0$ , góc tạo bởi phương quan sát ngọn cây và phương nằm ngang là $\small \widehat{FCE}=24^0$ . Ta cần tính DE.

Ta có hình minh hoạ:

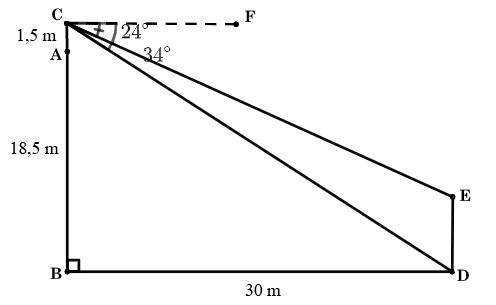
Vận dụng thực tiễn

Ta có: BC = BA + AC = 18,5 + 1,5 = 20 (m).

Tam giác BCD vuông tại B, áp dụng định lí Pythagore ta có:

CD² = BC² + BD² = 20² + 30² = 1300 (m)

$\small \Rightarrow CD=10\sqrt{3}$

Lại có: $\small \widehat{FCD}=\widehat{FCE}+\widehat{ECD}$

$\small \widehat{ECD}=\widehat{FCD}-\widehat{FCE}=34^0-24^0=10^0$

Mà CF // BD nên $\small \widehat{CDB}=\widehat{FCD}=34^0$ (so le trong)

$\small \Rightarrow \widehat{CDE}=90^0-\widehat{CDB}=90^0-34^0=56^0$

Xét ΔCDE có: $\small \widehat{ECD}+\widehat{CDE}+\widehat{CED}=180^0$ (định lí tổng ba góc trong tam giác)

$\small \widehat{CED}=180^0-(\widehat{ECD}+\widehat{CDE})$ = 180⁰ – (10⁰ + 56⁰) = 114⁰

Áp dụng định lí sin trong tam giác CDE ta có:

$\small \frac{CD}{sin\widehat{CED}}=\frac{DE}{sin\widehat{ECD}}$

$\small DE=\frac{CD.sin\widehat{ECD}}{sin\widehat{CED}}=\frac{10\sqrt{13}.sin10^0}{sin114^0}\approx 6,9(m)$

Vậy chiều cao của cây khoảng 6,9 m.

Trên đây KhoiA.Vn đã trình bày nội dung lý thuyết Công thức HERON tính diện tích tam giác, cách tính cạnh và góc tam giác? Toán 10 bài 2 SGK Cánh diều tập 1 chương 4 chi tiết, đầy đủ nhất. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết nhé, chúc các em thành công.