Bài 3 trang 120 SGK Toán 11 Tập 1 Chân trời sáng tạo
Cho hai hình vuông ABCD và ABEF ở hai mặt phẳng khác nhau...
Bài 3 trang 120 SGK Toán 11 tập 1 Chân trời sáng tạo: Cho hai hình vuông ABCD và ABEF ở hai mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD, AF tại M', N'.
a) Chứng minh (CBE)//(ADF)
b) Chứng minh (DEF)//(MNN'M')
Giải bài 3 trang 120 SGK Toán 11 tập 1 Chân trời sáng tạo:
Ta có hình vẽ minh hoạ sau:
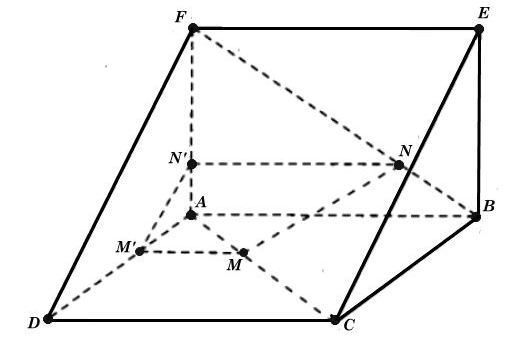
a) Ta có AD//BC ⇒ AD//(BEC)
AF//BE ⇒ AF//(BEC)
Mặt phẳng (ADF) đi qua hai đường thẳng cắt nhau AD và AF cùng song song với (CBE)
⇒ (ADF)//(CBE)
b) Vì ABCD và ABEF là hình vuông có cạnh bằng nhau nên: AC = BF
Xét tam giác ADC có MM'//CD nên
Xét tam giác ABF có NN'//AB nên
mà AM = BN nên
⇒ M'N'//DF. Nên M'N'//(DEF)
Ta có MM'//AB//EF nên MM'//(DEF)
Mặt phẳng (MNN'M') chứa hai đường thẳng cắt nhau MM' và M'N' cùng song song với (DEF)
Do đó, (MNN'M')//(DEF)
Trên đây KhoiA.Vn đã hướng dẫn các em giải bài 3 trang 120 SGK Toán 11 Tập 1 Chân trời sáng tạo. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết nhé, chúc các em thành công.
• Xem hướng dẫn giải bài tập Trang 119, 120 SGK Toán 11 Tập 1 Chân trời sáng tạo
Đánh giá & nhận xét
- Bài 8 trang 13 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 4 trang 141 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 3 trang 141 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 2 trang 141 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 1 trang 140 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 4 trang 135 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 3 trang 135 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 2 trang 135 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 1 trang 134 SGK Toán 11 Tập 1 Chân trời sáng tạo
- Bài 5 trang 126 SGK Toán 11 Tập 1 Chân trời sáng tạo




































