Dấu hiệu nhận biết Hình Thoi, tính chất, khái niệm Hình Thoi? Toán 8 bài 6 c5cd1

Dấu hiệu nhận biết Hình Thoi, tính chất, khái niệm Hình Thoi như thế nào? bài viết này sẽ cho các bạn lời giải đáp.

1. Khái niệm hình thoi

• Hình thoi là tứ giác có bốn cạnh bằng nhau.

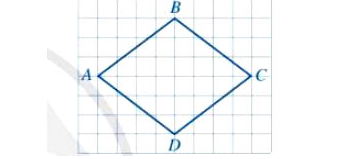
* Ví dụ: Ở hình sau, Tứ giác nào là hình thoi? vì sao?

* Lời giải:

Hình a) có MN = NP = PQ = QM = 2,5 nên tứ giác MNPQ là hình thoi.

Hình b) Vì KG ≠ GH nên tứ giác GHIK không phải hình thoi

2. Tính chất hình thoi

Trong một hình thoi:

- Các cạnh đối song song;

- Các góc đối bằng nhau;

- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

* Ví dụ: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O, AC = 3 cm, BD = 4 cm. Tính độ dài của OA, OB, AB.

* Lời giải:

Ta có hình minh hoạ như sau:

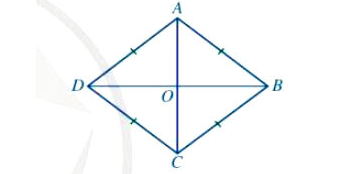
Do ABCD là hình thoi nên O là trung điểm của hai đường chéo AC, BD, nên có:

Ta có AC ⊥ BD (vì ABCD là hình thoi) nên tam giác OAB vuông tại O.

Áp dụng định lý Pythagore, ta có:

AB² = OA² + OB²

Do đó AB² = 1,5² + 2² = 6,25 hay AB = 2,5 (cm).

Vậy OA = 1,5 cm; OB = 2 cm; AB = 2,5 cm.

3. Dấu hiệu nhận biết hình thoi

Ta có dấu hiệu nhận biết:

- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

* Ví dụ: Cho tam giác ABC vuông tại A. Các điểm M, N lần lượt thuộc tia đối của tia AB, AC sao cho AM = AB, AN = AC. Chứng minh tứ giác BCMN là hình thoi.

* Lời giải:

Ta có hình minh hoạ như sau: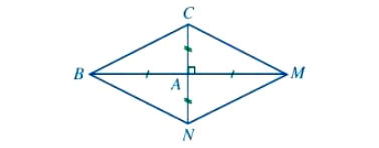

Tứ giác BCMN có A là trung điểm của hai đường chéo BM và CN nên BCMN là hình bình hành.

Do ΔABC vuông tại A nên   hay BM ⊥ CD.

Vậy hình BCMN có hai đường chéo BM và CN vuông góc với nhau nên BCMN là hình thoi.