Bài 3.17 trang 61 SGK Toán 8 tập 1 Kết nối tri thức

Bài 3.17 trang 61 Toán 8 Tập 1 Kết nối tri thức:

Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:

a) Hai tứ giác AEFD, AECF là những hình bình hành;

b) EF = AD, AF = EC.

Giải bài 3.17 trang 61 Toán 8 Tập 1 Kết nối tri thức:

Chúng ta có hình minh hoạ sau:

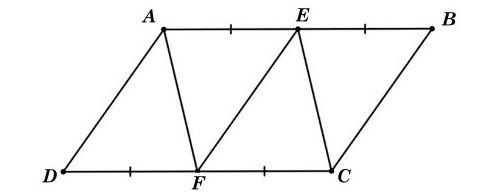
a) Hai tứ giác AEFD, AECF là những hình bình hành;

Vì ABCD là hình bình hành nên AB = CD, AB // CD.

Mà E, F lần lượt là trung điểm của AB, CD nên:

⇒ AE = BE = CF = DF.

• Xét tứ giác AEFD có:

AE // DF (vì AB // CD);

AE = DF (chứng minh trên)

⇒ Tứ giác AEFD là hình bình hành.

• Xét tứ giác AECF có:

AE // CF (vì AB // CD);

AE = CF (chứng minh trên)

⇒ Tứ giác AECF là hình bình hành.

Vậy hai tứ giác AEFD, AECF là những hình bình hành.

b) EF = AD, AF = EC.

Vì tứ giác AEFD là hình bình hành nên EF = AD.

Vì tứ giác AECF là hình bình hành nên AF = EC.

Vậy EF = AD, AF = EC.