Công thức nghiệm thu gọn của phương trình bậc 2 (b' với delta phẩy) - Toán 9 tập 2 bài 5

10:05:3204/03/2021

Ở bài trước các em đã biết công thức nghiệm của phương trình bậc 2, trường hợp nào thì phương trình bậc 2 có 2 nghiệm phân biệt, có nghiệm kép hay vô nghiệm.

Trong nhiều trường hợp, khi giải phương trình bậc hai nếu đặt b = 2b' thì việc tính toán để giải phương trình sẽ đơn giản hơn rất nhiều. Khi đặt b = 2b' ta có công thức nghiệm thu gọn của phương trình bậc 2.

1. Công thức nghiệm thu gọn của phương trình bậc 2

Đối với phương trình ax² + bx + c = 0 (a≠0) và b = 2b' biệt thức delta phẩy: Δ' = b'² - ac:

• Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt:

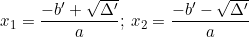
$\small x_1=\frac{-b'+\sqrt{\Delta' }}{a};\: x_2=\frac{-b'-\sqrt{\Delta' }}{a}$

• Nếu Δ' = 0 thì phương trình có nghiệm kép: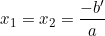 $\small x_1=x_2=\frac{-b'}{a}$

• Nếu Δ' < 0 thì phương trình vô nghiệm

* Lưu ý khi giải phương trình bậc 2:

- Khi a> và phương trình ax² + bx + c = 0 vô nghiệm thì biểu thức ax² + bx + c > 0 với mọi giá trị của x.

- Nếu phương trình ax² + bx + c = 0 có a<0 thì nên đổi dấu hai vế của phương trình để có a>0 để dễ giải hơn.

- Đối với phương trình bậc hai khuyết ax² + bx = 0 hay ax² + c = 0 nên dùng phép giải trực tiếp sẽ nhanh hơn là tính theo công thức nghiệm.

2. Bài tập vận dụng giải phương trình bậc 2

* Bài 17 trang 49 SGK Toán 9 Tập 2: Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:

a) 4x² + 4x + 1 = 0 ;

b) 13852x² – 14x + 1 = 0;

c) 5x² – 6x + 1 = 0;

d) -3x² + 4√6.x + 4 = 0.

* lời giải:

a) 4x² + 4x + 1 = 0

Phương trình bậc hai này có a = 4; b’ = 2; c = 1;

Δ’ = (b’)² – ac = 2² – 4.1 = 0

Phương trình có nghiệm kép là: 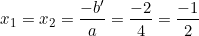$\small x_1=x_2=\frac{-b'}{a}=\frac{-2}{4}=\frac{-1}{2}$

b) 13852x² – 14x + 1 = 0

Phương trình bậc 2 này có: a = 13852; b’ = -7; c = 1;

Δ’ = (b’)² – ac = (-7)² – 13852.1 = -13803 < 0

Vậy phương trình vô nghiệm.

c) 5x² – 6x + 1 = 0

Phương trình bậc 2 này có: a = 5; b’ = -3; c = 1;

Δ’ = (b’)² – ac = (-3)² – 5.1 = 4 > 0

Phương trình có hai nghiệm phân biệt:

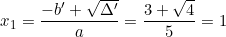
$\small x_1=\frac{-b'+\sqrt{\Delta '}}{a}=\frac{3+\sqrt{4}}{5}=1$

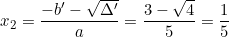
$\small x_2=\frac{-b'-\sqrt{\Delta '}}{a}=\frac{3-\sqrt{4}}{5}=\frac{1}{5}$

d) -3x² + 4√6.x + 4 = 0.

Phương trình này có a = -3; b' = 2√6; c = 4

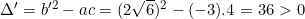
$\small \Delta '=b'^2-ac=(2\sqrt{6})^2-(-3).4=36>0$

Phương trình có hai nghiệm phân biệt:

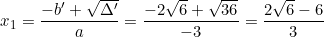
$\small x_1=\frac{-b'+\sqrt{\Delta '}}{a}=\frac{-2\sqrt{6}+\sqrt{36}}{-3}=\frac{2\sqrt{6}-6}{3}$

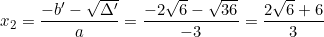
$\small x_2=\frac{-b'-\sqrt{\Delta '}}{a}=\frac{-2\sqrt{6}-\sqrt{36}}{-3}=\frac{2\sqrt{6}+6}{3}$

* Bài 18 trang 49 SGK Toán 9 Tập 2: Đưa các phương trình sau về dạng ax² + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):

a) 3x² – 2x = x² + 3;

b) (2x - √2)² – 1 = (x + 1)(x – 1);

c) 3x² + 3 = 2(x + 1);

d) 0,5x(x + 1) = (x – 1)².

* Lời giải:

a) 3x² – 2x = x² + 3 (*)

⇔ 3x² – 2x – x² – 3 = 0

⇔ 2x² – 2x – 3 = 0 (*)

Có a = 2; b’ = -1; c = -3; Δ’ = b’² – ac = (-1)² – 2.(-3) = 7 > 0

Phương trình (*) có hai nghiệm phân biệt:

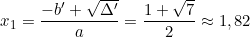
$\small x_1=\frac{-b'+\sqrt{\Delta '}}{a}=\frac{1+\sqrt{7}}{2}\approx 1,82$

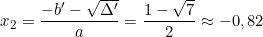
$\small x_2=\frac{-b'-\sqrt{\Delta '}}{a}=\frac{1-\sqrt{7}}{2}\approx -0,82$

b) (2x - √2)² – 1 = (x + 1)(x – 1);

⇔ 4x² – 2.2x.√2 + 2 – 1 = x² – 1

⇔ 4x² – 2.2√2.x + 2 – 1 – x² + 1 = 0

⇔ 3x² – 2.2√2.x + 2 = 0

Có: a = 3; b’ = -2√2; c = 2; Δ’ = b’² – ac = (-2√2)² – 3.2 = 2 > 0

Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:

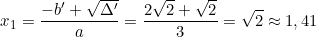
$\small x_1=\frac{-b'+\sqrt{\Delta '}}{a}=\frac{2\sqrt{2}+\sqrt{2}}{3}=\sqrt{2}\approx 1,41$

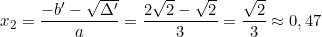
$\small x_2=\frac{-b'-\sqrt{\Delta '}}{a}=\frac{2\sqrt{2}-\sqrt{2}}{3}=\frac{\sqrt{2}}{3}\approx 0,47$

c) 3x² + 3 = 2(x + 1)

⇔ 3x² + 3 = 2x + 2

⇔ 3x² + 3 – 2x – 2 = 0

⇔ 3x² – 2x + 1 = 0

Phương trình có a = 3; b’ = -1; c = 1; Δ’ = b’² – ac = (-1)² – 3.1 = -2 < 0

Vậy phương trình vô nghiệm.

d) 0,5x(x + 1) = (x – 1)²

⇔ 0,5x² + 0,5x = x² – 2x + 1

⇔ x² – 2x + 1 – 0,5x² – 0,5x = 0

⇔ 0,5x² – 2,5x + 1 = 0

⇔ x² – 5x + 2 = 0

Phương trình có: a = 1; b' = -5/2; c = 2.

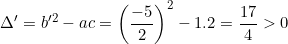
$\small \Delta '=b'^2-ac=\left ( \frac{-5}{2} \right )^2-1.2=\frac{17}{4}>0$

Phương trình có hai nghiệm phân biệt:

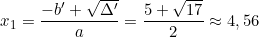
$\small x_1=\frac{-b'+\sqrt{\Delta '}}{a}=\frac{5+\sqrt{17}}{2}\approx 4,56$

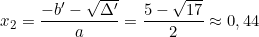
$\small x_2=\frac{-b'-\sqrt{\Delta '}}{a}=\frac{5-\sqrt{17}}{2}\approx 0,44$

* Bài 19 (trang 49 SGK Toán 9 Tập 2): Đố. Đố em biết vì sao khi a > 0 và phương trình ax² + bx + c = 0 vô nghiệm thì ax² + bx + c > 0 với mọi giá trị của x?

* Lời giải:

- Ta có: 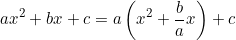$\small ax^2+bx+c=a\left ( x^2+\frac{b}{a}x \right )+c$

$\small =\left [ x^2+2.x.\frac{b}{2a}+\left ( \frac{b}{2a} \right )^2-\left ( \frac{b}{2a} \right )^2 \right ]+c$

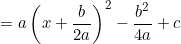
$\small =a\left [ \left ( x+\frac{b}{2a} \right )^2-\frac{b^2}{4a^2} \right ]+c$ $\small =a \left ( x+\frac{b}{2a} \right )^2-\frac{b^2}{4a} +c$

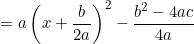
$\small =a \left ( x+\frac{b}{2a} \right )^2-\frac{b^2-4ac}{4a}$

- Theo bài ra, a >0, 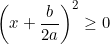$\small \left ( x+\frac{b}{2a} \right )^2\geq 0$ với mọi x, a, b nên suy ra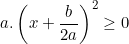 $\small \small a.\left ( x+\frac{b}{2a} \right )^2\geq 0$

Phương trình ax² + bx + c = 0 vô nghiệm nên

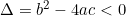$\small \Delta =b^2-4ac<0$ mà a > 0 nên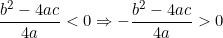 $\small \frac{b^2-4ac}{4a}<0\Rightarrow -\frac{b^2-4ac}{4a}>0$

Vậy 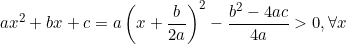$\small ax^2+bx+c=a\left ( x+\frac{b}{2a} \right )^2-\frac{b^2-4ac}{4a}>0,\forall x$

Tóm lại, với bài viết này các em cần ghi nhớ được công thức nghiệm thu gọn của phương trình bậc 2 với b' và delta phẩy. Khi delta phẩy > 0 phương trình có 2 nghiệm, delta phẩy = 0 phương trình có nghiệm kép, delta phẩy < 0 thì phương trình vô nghiệm.

Công thức nghiệm thu gọn của phương trình bậc 2 (b' với delta phẩy) - Toán 9 tập 2 bài 5

Tags

Đánh giá & nhận xét