Công thức nghiệm của phương trình bậc 2 một ẩn, lý thuyết và bài tập - Toán 9 tập 2 bài 4
Ở bài trước các em đã biết dạng tổng quát của phương trình bậc 2 một ẩn, đồng thời cũng biết cách giải phương trình bậc 2 này bằng cách phân tích thành nhân tử hoặc đưa về dạng hằng đẳng thức để giải.
Bài viết này sẽ giới thiệu cho chúng ta một phương pháp để giải phương trình bậc 2 và được gọi là công thức nghiệm của phương trình bậc 2. Qua công thức nghiệm này chúng ta sẽ làm các bài tập vận dụng để các em hiểu rõ hơn.
1. Công thức nghiệm của phương trình bậc 2
Đối với phương trình ax2 + bx + c = 0 (a≠0) và biệt thức delta: Δ = b2 - 4ac:
• Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt:
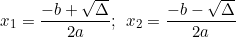 ;
;
• Nếu Δ = 0 thì phương trình có nghiệm kép: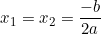 ;
;
• Nếu Δ < 0 thì phương trình vô nghiệm
2. Bài tập vận dụng giải phương trình bậc 2
* Bài 15 trang 45 SGK Toán 9 Tập 2: Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
a) 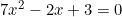
b) 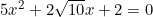
c) 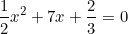
d) 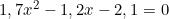
* lời giải:
a) 7x2 – 2x + 3 = 0
Phương trình bậc hai này có: a = 7; b = -2; c = 3;
Tính biệt thức delta: Δ = b2 – 4ac = (-2)2 – 4.7.3 = -80 < 0
→Vậy phương trình vô nghiệm.
b) 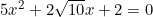
Phương trình bậc hai này có: a = 5; b = 2√10; c = 2.
Tính biệt thức delta: Δ = b2 – 4ac = (2√10)2 – 4.2.5 = 0
→Vậy phương trình có nghiệm kép.
c) 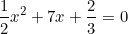
Phương trình bậc hai này có: a = 1/2; b = 7; c = 2/3.
Tính biệt thức delta: Δ = b2 – 4ac = 72 - 4.(1/2).(2/3) = 143/3 >0.
→Vậy phương trình có 2 nghiệm phân biệt.
d) 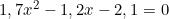
Phương trình bậc hai này có: a = 1,7; b = -1,2; c = -2,1.
Tính biệt thức delta: Δ = b2 – 4ac = (-1,2)2 – 4.1,7.(-2,1) = 15,72 > 0.
→Vậy phương trình có 2 nghiệm phân biệt.
* Bài 16 trang 45 SGK Toán 9 Tập 2: Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a) 2x2 – 7x + 3 = 0; b) 6x2 + x + 5 = 0;
c) 6x2 + x – 5 = 0; d) 3x2 + 5x + 2 = 0;
e) y2 – 8y + 16 = 0; f) 16z2 + 24z + 9 = 0.
* Lời giải:
a) 2x2 – 7x + 3 = 0
Phương trình bậc hai này có: a = 2; b = -7; c = 3;
Δ = b2 – 4ac = (-7)2 – 4.2.3 = 25 > 0
Vậy phương trình có hai nghiệm phân biệt là:
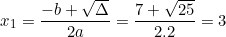
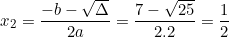
b) 6x2 + x + 5 = 0
Phương trình bậc hai này có a = 6; b = 1; c = 5;
Δ = b2 – 4ac = 12 – 4.5.6 = -119 < 0
Vậy phương trình vô nghiệm.
c) 6x2 + x – 5 = 0
Phương trình bậc hai này có a = 6; b = 1; c = -5;
Δ = b2 – 4ac = 12 – 4.6.(-5) = 121 > 0
Phương trình có hai nghiệm phân biệt là:
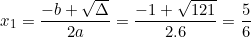
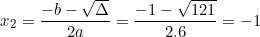
d) 3x2 + 5x + 2 = 0
Phương trình bậc hai này có a = 3; b = 5; c = 2;
Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Phương trình có hai nghiệm phân biệt là:
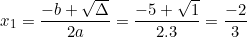
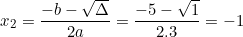
e) y2 – 8y + 16 = 0
Phương trình bậc hai này có a = 1; b = -8; c = 16;
Δ = b2 – 4ac = (-8)2 – 4.1.16 = 0.
Phương trình có nghiệm kép: 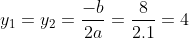
f) 16z2 + 24z + 9 = 0
Phương trình bậc hai này có a = 16; b = 24; c = 9;
Δ = b2 – 4ac = 242 – 4.16.9 = 0
Phương trình có nghiệm kép: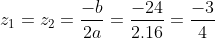
Tóm lại, với bài viết này các em cần ghi nhớ được công thức nghiệm của phương trình bậc 2, và khi delta > 0 phương trình có 2 nghiệm, delta = 0 phương trình có nghiệm kép, delta < 0 thì phương trình vô nghiệm.
Đánh giá & nhận xét
- Xác định công thức phân tử (lập CTPT) hợp chất hữu cơ lớp 9 - Hỏi đáp môn Hoá
- Bài tập về Nhiên liệu: Giải bài 1, 2, 3, 4 trang 132 SGK Hoá 9
- Nhiên liệu là gì? Nhiên liệu được phân loại như thế nào? cách sử dụng nhiên liệu hiểu quả - Hoá 9 bài 41
- Bài tập về Dầu mỏ và Khí thiên nhiên: Giải bài 1, 2, 3, 4 trang 129 SGK Hoá 9
- Tính chất vật lý, trạng thái tự nhiên của dầu mỏ ứng dụng của dầu mỏ và khí tiên nhiên - Hoá 9 bài 40
- Bài tập về Benzen C6H6: Giải bài 1, 2, 3, 4 trang 125 SGK Hoá 9
- Bài tập về Axetilen C2H2: Giải bài 1, 2, 3, 4, 5 trang 122 SGK Hoá 9
- Bài tập về Etilen C2H4: Giải bài 1, 2, 3, 4 trang 119 SGK Hoá 9
- Bài tập về Metan CH4: Giải bài 1, 2, 3, 4 trang 116 SGK Hoá 9
- Tính chất vật lý, Tính chất hóa học của Metan CH4 và Ứng dụng - Hóa 9 bài 36


































