Cách chứng minh 5 điểm (các điểm) cùng nằm trên một đường tròn lớp 9? Hỏi nhanh đáp gọn môn Toán

Tuy nhiên, vẫn có một số bạn chưa biết Cách chứng minh 5 điểm (các điểm) cùng nằm trên một đường tròn như thế nào. Bài viết này sẽ giúp các bạn thấy việc chứng minh 5 điểm cùng thuộc một đường tròn không hề khó.

1. Cách chứng minh 5 điểm cùng nằm trên một đường tròn

* Cách 1: Chứng minh các điểm (5 điểm) đó cùng cách đều một điểm O cố định. Khi đó các điểm đã cho cùng thuộc đường tròn tâm O.

* Cách 2: Sử dụng tứ giác nội tiếp. Chẳng hạn để chứng minh 5 điểm M, A, O, B, C cùng thuộc một đường tròn ta chứng minh MAOB, MAOC là tứ giác nội tiếp cùng 1 đường tròn tâm I.

2. Ví dụ minh họa cách chứng mình 5 điểm cùng thuộc một đường tròn.

* Ví dụ 1: Cho hình chữ nhật ABCM vẽ tam giác AEC vuông tại E. Chứng minh 5 điểm A, B, C, M, E cùng thuộc một đường tròn.

* Lời giải:

Ta có hình minh họa như sau:

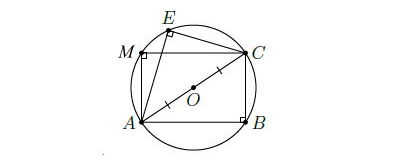
Gọi O là trung điểm của AC

Vì ΔABC vuông tại B nên 3 điểm A, B, C thuộc đường tròn tâm O đường kính AC

Vì ΔACM vuông tại B nên 3 điểm A, C, M thuộc đường tròn tâm O đường kính AC

Vì ΔACE vuông tại B nên 3 điểm A, C, E thuộc đường tròn tâm O đường kính AC

Vậy 5 điểm A, B, C, M, E cùng thuộc đường tròn tâm O đường kính AC.

* Ví dụ 2: Cho tam giác ABC vuông tại A, đường cao AH. Từ M là điểm bất kì trên cạnh BC kẻ MD ⊥ AB, ME ⊥ AC. Chứng minh 5 điểm A, D, M, H, E cùng thuộc một đường tròn.

* Lời giải:

- Theo bài ra, có có hình sau:

Xét tam giác vuông ADM có cạnh huyền AM

Xét tam giác vuông AEM có cạnh huyền AM

Và tam giác vuông AHM có cạnh huyền AM

Các tam giác này đều có chung cạnh huyền AM nên 3 đỉnh góc vuông nằm trên đường tròn đường kính AM có tâm là trung điểm của AM.

Vậy 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.

* Ví dụ 3: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.

* Lời giải:

- Ta có hình vẽ như sau:

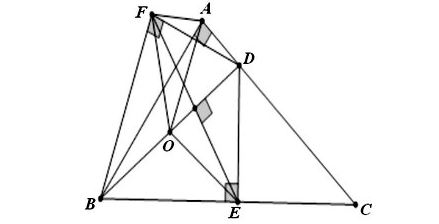- Theo giả thuyết, DE ⊥ BC nên ∠BEB = 90⁰

- Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF nên suy ra:

 BF = BE và DF = DE

Suy ra: ΔBFD = ΔBED (c-c-c)

Suy ra: ∠BFD = ∠BEB = 90⁰

- Gọi O là trung điểm của BD.

- Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên:

 AO = ½BD = OB = OD   (1)

- Xét tam giác vuông BDE vuông tại E có OE là trung tuyến nên:

 EO = ½BD = OB = OD   (2)

- Xét tam giác vuông BFD vuông tại F có OF là trung tuyến nên:

 FO = ½BD = OB = OD   (3)

Từ (1), (2) và (3) suy ra: OA = OB = OD = OE = OF.

Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC.