Bài tập về Hàm số, đồ thị hàm số, hàm số đồng biến, nghịch biến cơ bản - Toán 9 bài 1

17:27:2110/10/2021

Sau khi đã tìm hiểu nội dung lý thuyết về hàm số, đồ thị hàm số, hàm đồng biến và hàm nghịch biến thì bài viết này chúng ta sẽ vận dụng vào giải các bài tập cụ thể.

Bài tập về hàm số Hàm số, đồ thị hàm số, hàm số đồng biến, nghịch biến có một số dạng như bản như: Tính giá trị của hàm số tại một điểm; Xét sự đồng biến và nghịch biến của hàm số;...

* Bài 1 trang 44 SGK Toán 9 Tập 1: a) Cho hàm số $\small y=f(x)=\frac{2}{3}x$

Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3).

b) Cho hàm số $\small y=g(x)=\frac{2}{3}x+3$

Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3).

c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?

> Lời giải:

a) Tính các giá trị như sau:

$\small f(-2)=\frac{2}{3}(-2)=-\frac{4}{3}$

$\small f(-1)=\frac{2}{3}(-1)=-\frac{2}{3}$

$\small f(0)=\frac{2}{3}.0=0$

$\small f(\frac{1}{2})=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}$

$\small f(1)=\frac{2}{3}.1=\frac{2}{3}$

$\small \small f(2)=\frac{2}{3}.2=\frac{4}{3}$

$\small \small f(3)=\frac{2}{3}.3=2$

b) Tính các giá trị như sau:

$\small g(-2)=\frac{2}{3}.(-2)+3=-\frac{4}{3}+3=\frac{5}{3}$

$\small g(-1)=\frac{2}{3}.(-1)+3=-\frac{2}{3}+3=\frac{7}{3}$

$\small g(0)=\frac{2}{3}.0+3=3$

$\small g(\frac{1}{2})=\frac{2}{3}.\frac{1}{2}+3=\frac{1}{3}+3=\frac{10}{3}$

$\small \small g(1)=\frac{2}{3}.1+3=\frac{2}{3}+3=\frac{11}{3}$

$\small g(2)=\frac{2}{3}.2+3=\frac{4}{3}+3=\frac{13}{3}$

$\small g(3)=\frac{2}{3}.3+3=2+3=5$

c) Từ kết quả câu a) và b) ta có bảng:

x	-2	-1	0	1/2	1	2	3
y=f(x) = (2/3)x	-4/3	-2/3	0	1/3	2/3	4/3	2
y=g(x) = (2/3)x + 3	(-4/3)+3	(-2/3)+3	0+3	(1/3)+3	(2/3)+3	(4/3)+3	2+3

> Nhận xét:

- Hai hàm số $\small y=f(x)=\frac{2}{3}x$ và $\small y=g(x)=\frac{2}{3}x+3$

là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng.

- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.

(Có thể thấy rằng g(x) = f(x) + 3)

* Bài 2 trang 45 SGK Toán 9 Tập 1: Cho hàm số $\small y=-\frac{1}{2}x+3$

a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:

x	-2,5	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2	2,5
y=(-1/2)x+3

b) Hàm số đã cho là hàm số đồng biến hay nghịch biến? Vì sao?

> Lời giải:

a) Tính các giá trị như sau:

$\small x=-2,5\Rightarrow y=-\frac{1}{2}.(-2,5)+3=4,25$

$\small x=-2\Rightarrow y=-\frac{1}{2}.(-2)+3=4$

$\small x=-1,5\Rightarrow y=-\frac{1}{2}.(-1,5)+3=3,75$

$\small x=-1\Rightarrow y=-\frac{1}{2}.(-1)+3=3,5$

$\small x=-0,5\Rightarrow y=-\frac{1}{2}.(-0,5)+3=3,25$

$\small x=0\Rightarrow y=-\frac{1}{2}.0+3=3$

$\small x=0,5\Rightarrow y=-\frac{1}{2}.0,5+3=2,75$

$\small x=1\Rightarrow y=-\frac{1}{2}.1+3=2,5$

$\small x=1,5\Rightarrow y=-\frac{1}{2}.(1,5)+3=2,25$

$\small x=2\Rightarrow y=-\frac{1}{2}.2+3=2$

$\small x=2,5\Rightarrow y=-\frac{1}{2}.(2,5)+3=1,75$

Ta có được bảng sau:

x	-2,5	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2	2,5
y=(-1/2)x+3	4,25	4	3,75	3,5	3,25	3	2,75	2,5	2,25	2	1,75

b) Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.

* Bài 3 trang 45 SGK Toán 9 Tập 1: Cho hai hàm số y = 2x và y = -2x

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.

b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?

> Lời giải:

a) - Với hàm số y = 2x

Bảng giá trị:

x	0	1
y = 2x	0	2

Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)

- Với hàm số y = -2x

Bảng giá trị:

x	0	1
y = -2x	0	-2

Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B(1; - 2)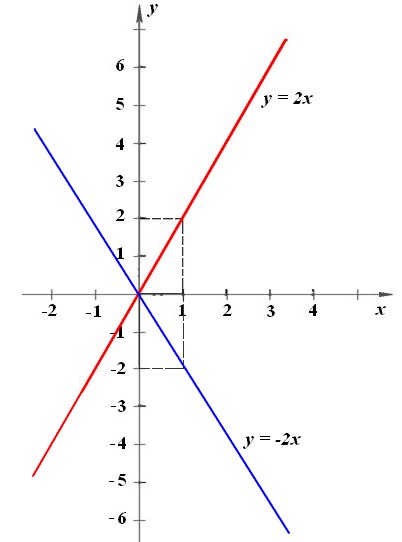 Đồ thị hàm số y = 2x và y = -2x trên cùng trục tọa độ

b) Ta có O(x₁ = 0, y₁ = 0) và A(x₂ = 1, y₂ = 2) thuộc đồ thị hàm số y = 2x, nên với x₁ < x₂ ta được f(x₁) < f(x₂).

Vậy hàm số y = 2x đồng biến trên R.

Lại có O(x₁ = 0, y₁ = 0) và B(x₃ = 1, y₃ = -2) thuộc đồ thị hàm số y = -2x, nên với x₁ < x₃ ta được f(x₁) < f(x₃).

Vậy hàm số y = -2x nghịch biến trên R.

Nếu có nhận xét về nội dung phần Bài tập về Hàm số, đồ thị hàm số, hàm số đồng biến, nghịch biến cơ bản ở trên, các em hãy để lại ở phần bình luận dưới bài viết nhé, KhoiA.Vn chúc các em thành công.

Bài tập về Hàm số, đồ thị hàm số, hàm số đồng biến, nghịch biến cơ bản - Toán 9 bài 1

Tags

Đánh giá & nhận xét