Bài tập tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn - Giải tích 12 bài 3

12:02:5919/07/2021

Ở bài trước các em đã biết để tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số trên một đoạn chúng ta thực hiện qua 3 bước cơ bản.

Trong bài viết này chúng ta sẽ vận dụng 3 bước của quy tắc tìm giá trị lớn nhất nhỏ nhất này để giải một số bài tập tìm GTLN, GTNN của một số hàm có chứa dấu căn thức, dấu giá trị tuyệt đối và hàm chứa ẩn dưới mẫu số.

• Lý thuyết cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một đoạn

* Bài 1 trang 23,24 SGK Giải tích 12: Tính giá trị lớn nhất và nhỏ nhất của hàm số:

a) y = x³ - 3x² - 9x + 35 trên các đoạn [-4; 4] và [0; 5];

b) y = x⁴ - 3x² + 2 trên các đoạn [0; 3] và [2; 5];

c) $\small y=\frac{2-x}{1-x}$ trên các đoạn [2 ; 4] và [-3 ; -2];

d) $\small y=\sqrt{5-4x}$ trên đoạn [-1 ; 1].

> Lời giải:

a) y = x³ - 3x² - 9x + 35 trên các đoạn [-4; 4] và [0; 5];

- TXĐ: D = R.

- Ta có: y' = 3x² - 6x - 9;

y' = 0 ⇔ x = –1 hoặc x = 3.

¤ Xét hàm số trên đoạn [-4; 4]:

y(-4) = -41; y(-1) = 40; y(3) = 8; y(4) = 15.

$\small \underset{[-4;4]}{min}y = min \left \{ y(-4);y(-1);y(3);y(4)\right \}$

$\small =min\left \{ -41;40;8;15 \right \}=-41$

$\small \underset{[-4;4]}{max}y = y(-1)=40$

¤ Xét hàm số trên [0 ; 5].

y(0) = 35; y(3) = 8; y(5) = 40.

$\small \Rightarrow \underset{[0;5]}{min}y = y(3)=8$

$\small \Rightarrow \underset{[0;5]}{max}y = y(5)=40$

b) y = x⁴ - 3x² + 2 trên các đoạn [0; 3] và [2; 5];

- TXĐ: D = R

- Ta có: y' = 4x³ - 6x

y’ = 0 ⇔ 2x.(2x² – 3) = 0 ⇔ x = 0 hoặc $\small x=\pm \sqrt{\frac{3}{2}}$

¤ Xét hàm số trên đoạn [0; 3]:

y(0) = 2; y((√3)/2) = -1/4; y(3) = 56.

$\small \Rightarrow \underset{[0;3]}{min}y = y\left ( \sqrt{\frac{3}{2}} \right )=\frac{-1}{4}$

$\small \Rightarrow \underset{[0;3]}{max}y = y\left (3 \right )=56$

¤ Xét hàm số trên [2; 5].

y(2) = 6; y(5) = 552.

$\small \Rightarrow \underset{[2;5]}{min}y = y(2)=6$

$\small \Rightarrow \underset{[2;5]}{max}y = y(5)=552$

c) $\small y=\frac{2-x}{1-x}$ trên các đoạn [2 ; 4] và [-3 ; -2];

- TXĐ: D = (-∞; 1) ∪ (1; +∞)

- Ta có: $\small y'=\frac{1}{(1-x)^2}>0,\: \forall x\in D$

⇒ hàm số đồng biến trên (-∞; 1) và (1; +∞).

⇒ Hàm số đồng biến trên [2; 4] và [-3; -2].

$\small \Rightarrow \underset{[2;4]}{min}y = y(2)=0$

$\small \Rightarrow \underset{[2;4]}{max}y = y(4)=\frac{2}{3}$

d) $\small y=\sqrt{5-4x}$ trên đoạn [-1 ; 1]

- TXĐ: D = (-∞; 5/4]

$\small y'=\frac{-2}{\sqrt{5-4x}}<0,\: \forall x\in D$

⇒ Hàm số nghịch biến trên (-∞; 5/4)

⇒ Hàm số nghịch biến trên [-1; 1]

$\small \Rightarrow \underset{[-1;1]}{min}y = y(1)=1$

$\small \Rightarrow \underset{[-1;1]}{max}y = y(-1)=3$

* Bài 2 trang 24 SGK Giải tích 12: Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

> Lời giải:

- Theo bài ra, nửa chu vi hình chữ nhật là: 16:2 = 8cm.

- Gọi độ dài 1 cạnh của hình chữ nhật là x (cm)

⇒ Độ dài cạnh còn lại là : 8 – x (cm)

⇒ Diện tích của hình chữ nhật là:

S = x(8 – x) = 8x – x² = 16 – (16 – 8x + x²) = 16 – (x – 4)² ≤ 16.

⇒ S_max = 16, dấu bằng xảy ra khi (x – 4)² = 0 ⇔ x = 4.

Vậy trong các hình chữ nhật có chu vi 16cm thì hình chữ nhật có ạnh bằng 4cm có diện tích lớn nhất bằng 16cm². Khi đó hình chữ nhật này chính là hình vuông.

* Bài 3 trang 24 SGK Giải tích 12: Trong tất cả các hình chữ nhật có diện tích 48 m², hãy xác định hình chữ nhật có chu vi nhỏ nhất.

> Lời giải:

- Gọi độ dài của một cạnh của hình chữ nhật là x (m) (x > 0).

⇒ Độ dài cạnh còn lại là: 48/x (m)

⇒ chu vi hình chữ nhật là: $\small C_{hcn}(x)=2.\left ( x+\frac{48}{x} \right )=2x+\frac{96}{x}$

Xét hàm C(x) ở trên khoảng (0; +∞) có: $\small C'(x)=2-\frac{96}{x^2}$

$\small C'(x)=0\Leftrightarrow 2-\frac{96}{x^2}=0$ $\small \Leftrightarrow x^2=48\Leftrightarrow x=4\sqrt{3}$

- Bảng biến thiên trên (0; +∞):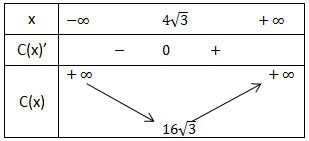 bảng biến thiên bài 3 trang 24 sgk giải tích 12

$\small \Rightarrow \underset{(0;+\infty )}{min}C(x)=C(4\sqrt{3})=16\sqrt{3}$

Vậy trong các hình chữ nhật có cùng diện tích 48m² thì hình vuông cạnh 4√3 (m) có chu vi nhỏ nhất.

* Bài 4 trang 24 SGK Giải tích 12: Tính giá trị lớn nhất của các hàm số sau:

a) $\small y=\frac{4}{1+x^2}$

b) y = 4x³ - 3x⁴

> Lời giải:

a) $\small y=\frac{4}{1+x^2}$

- TXĐ: D = R.

- Ta có: $y'=\frac{-8x}{(1+x^2)^2}\Rightarrow y'=0$

$\Leftrightarrow 8x=0\Leftrightarrow x=0$

- Bảng biến thiên: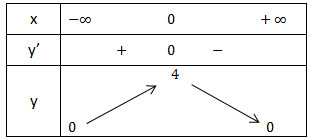 bbt bài 4 câu a trang 24 sgk giải tích 12

Từ bảng biến thiên ta thấy hàm số đạt GTLN tại x = 0, y_max = 4;

+ Với câu này ta có thêm một cách khác, làm như sau:

Ta thấy, 1 + x² ≥ 1 với mọi x nên: $\small \frac{4}{1+x^2} \leq \frac{4}{1}=4$ ⇒ y ≤ 4.

Vậy maxy = 4, dấu "=" xảy ra khi x = 0.

b) y = 4x³ - 3x⁴

- TXĐ: D = R.

- Ta có: y' = 12x² - 12x³ = 12x²(1 - x)

y' = 0 ⇔ x = 0 hoặc x = 1

Bảng biến thiên: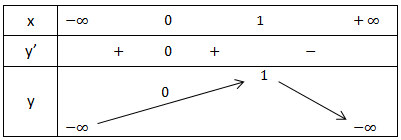 bảng biến thiên bài 4 câu b

Theo bảng biến thiên ta thấy hàm số đạt GTLN tại x = 1, y_max = 1.

* Bài 5 trang 24 SGK Giải tích 12: Tính giá trị nhỏ nhất của các hàm số sau:

a) y = |x|

b) $\small y=x+\frac{1}{x}\: \: (x>0)$

> Lời giải:

a) y = |x|

Đối với câu này, ta có thể giải theo 2 cách:

+ Cách 1: Ta có: y = |x| ≥ 0 ∀ x

⇒ Hàm số có giá trị nhỏ nhất là min y = 0 khi x = 0.

+ Cách 2: Ta có:

$\small y=|x|=\left\{\begin{matrix} x\: \: khi\: x\in [0;+\infty )\\ -x\: \: khi\: x\in (-\infty ;0) \end{matrix}\right.$

và $\small y'=\left\{\begin{matrix} 1\: \: khi\: x>0\\ -1\: \: khi\: x<0 \end{matrix}\right.$

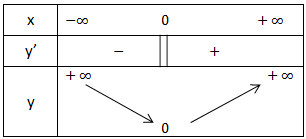
- Bảng biến thiên: bảng biến thiên bài 5 câu a

Từ bảng biến thiên ta có hàm số đạt GTNN tại x = 0, y_min = 0.

b) $\small y=x+\frac{1}{x}\: \: (x>0)$

- Ta có: $\small y'=1-\frac{4}{x^2};\: y'=0\Leftrightarrow 1-\frac{4}{x^2}=0$

$\small \Leftrightarrow x^2=4\Leftrightarrow \left \[\begin{matrix} x=2\\ x=-2 \end{matrix} \right.$

Ta thấy x = 2 thỏa, x = -2 ∉ (0;+∞).

- Bảng biến thiên: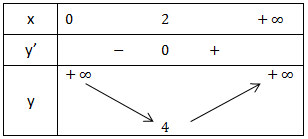
bảng biến thiên bài 5 câu b

Từ bảng biến thiên suy ra $\small \underset{(0;+\infty )}{min}y=4$ khi x = 2.

+ Với câu này ta có thể áp dụng bất đẳng thức Cô-si vì x>0 nên:

$\small y=x+\frac{4}{x}\geq 2\sqrt{x.\frac{4}{x}}=4\Rightarrow y\geq 4$

Dấu "=" xảy ra khi $\small x=\frac{4}{x}\Leftrightarrow x^2=4\Leftrightarrow x=2\: (v\grave{i}\: x>0)$

suy ra: miny = 4 khi x = 2.

Trên đây là bài viết hướng dẫn giải một số Bài tập tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn. KhoiA hy vọng qua bài viết này các em có thể hiểu rõ cách giải các bài tập tìm GTLN, GTNN của một số hàm có chứa dấu căn thức, dấu giá trị tuyệt đối và hàm chứa ẩn dưới mẫu số.

Bài tập tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn - Giải tích 12 bài 3

Tags

Đánh giá & nhận xét