Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn - Giải tích 12 bài 3
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn là bài toán các em rất hay gặp trong đề thi tốt nghiệp THPT quốc gia, vì vậy đừng bỏ lỡ khi gặp dạng này nhé.
Bài này sẽ giúp các em biết cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một đoạn (trong miền giá trị).
• Bài tập cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một đoạn
I. Định nghĩa giá trị lớn nhất giá trị nhỏ nhất
Cho hàm số y = f(x) xác định trên tập D.
• Số M là giá trị lớn nhất (GTLN) của hàm số f(x) trên D nếu f(x) ≤ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M.
Ký hiệu:
• Số m là giá trị nhỏ nhất (GTNN) của hàm số f(x) trên D nếu f(x) ≥ m với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = m.
Ký hiệu:
* Ví dụ: Tìm giá trị lớn nhất, nhỏ nhất của hàm số
trên khoảng (0;+∞)
> Lời giải:
- Trên khoảng (0;+∞), ta có:
- Bảng biến thiên: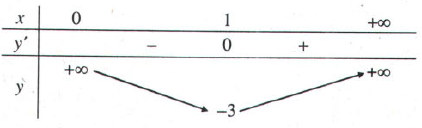 Từ BBT ta thấy trên khoảng (0;+∞) hàm số có giá trị cực tiểu duy nhất, đó cũng là giá trị nhỏ nhất của hàm số.
Từ BBT ta thấy trên khoảng (0;+∞) hàm số có giá trị cực tiểu duy nhất, đó cũng là giá trị nhỏ nhất của hàm số.
Vậy tại x = 1. Không tồn tại giá trị lớn nhất của f(x) trên khoảng (0;+∞).
II. Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
• Định lý:
- Hàm số liên tục trên một đoạn thì có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
• Quy tắc tìm GTLN, GTNN của hàm số y = f(x) liên tục trên đoạn [a ; b]
+ Bước 1: Tìm các điểm xi ∈ (a ; b)(i = 1, 2, . . . , n) mà tại đó f'(xi) = 0 hoặc f'(xi) không xác định.
+ Bước 2: Tính f(a), f(b), f(xi) (i = 1, 2, . . . , n) .
+ Bước 3: Tìm
> Chú ý: Cũng như ở mục I. Để tìm GTLN, GTNN của hàm số y=f(x) xác định trên tập hợp D, ta có thể khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số mà kết luận về GTLN và GTNN của hàm số.
- Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất (các em lưu ý sự khác biệt một khoảng và một đoạn).
* Ví dụ 1: Cho hàm số:
có đồ thị như Hình 10 (hình dưới). Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.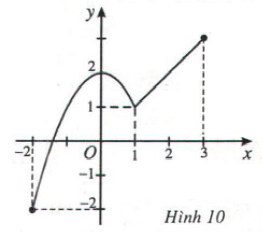
> Lời giải:
- Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2.
Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
- Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3.
Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.
* Ví dụ 2: Lập bảng biến thiên hàm số
Từ đó suy ra giá trị nhỏ nhất của f(x) trên tập xác định.
> Lời giải:
- TXĐ: D = R.
- Ta có: y' = 2x/(1 + x2)2 . Cho y' = 0 thì x = 0.
- Bảng biến thiên: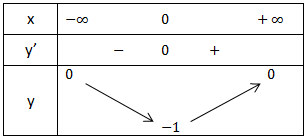 ⇒ Vậy giá trị nhỏ nhất của hàm số đã cho bằng –1 tại x = 0.
⇒ Vậy giá trị nhỏ nhất của hàm số đã cho bằng –1 tại x = 0.
Trên đây là nội dung lý thuyết về Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn. KhoiA hy vọng các em đã hiểu rõ và có thể vận dụng giải các bài tập liên quan, chúc các em học tốt. Mọi góp ý các em hãy để lại bình luận dưới bài viết.
Đánh giá & nhận xét
- Giải Địa lí 12 trang 23 Chân trời Sáng tạo
- Giải Địa lí 12 trang 27 Chân trời Sáng tạo
- Giải Địa lí 12 trang 26 Chân trời Sáng tạo
- Giải Địa lí 12 trang 25 Chân trời Sáng tạo
- Giải Địa lí 12 trang 22 Chân trời Sáng tạo
- Giải Địa lí 12 trang 21 Chân trời Sáng tạo
- Giải Địa lí 12 trang 20 Chân trời Sáng tạo
- Giải Địa lí 12 trang 19 Chân trời Sáng tạo
- Giải Địa lí 12 trang 18 Chân trời Sáng tạo
- Giải Địa lí 12 trang 16 Chân trời Sáng tạo


































