Lũy thừa là gì? Tính chất của lũy thừa với số mũ thực, căn bậc n và tính chất căn bậc n - Toán 12 bài 1

19:42:3016/10/2021

Lũy thừa là khái niệm không còn xa lạ với các em bởi chúng ta đã làm quen từ lớp 6. Trong toán giải tích 12 khái niệm lũy thừa sẽ được chúng ta tìm hiểu sâu hơn.

Bài viết dưới đây chúng ta sẽ cùng tìm hiểu khái niệm lũy thừa, lũy thừa với số mũ nguyên, hữu tỉ, vô tỉ và số mũ thực; về phương trình xⁿ = a, căn bậc n và tính chất của căn bậc n.

I. Khái niệm lũy thừa

1. Lũy thừa với số mũ nguyên

- Cho n là một số nguyên dương.

- Với a là một số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.

aⁿ = a.a.a......a (n thừa số a)

Với a ≠ 0 thì a⁰ = 1, $\small a^{-n}=\frac{1}{a^n}$

> Chú ý: 0ⁿ và 0^-n không có nghĩa

Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.

2. Căn bậc n

a) Định nghĩa căn bậc n

- Cho số thực b và số nguyên dương n (n ≥ 2). Số a được gọi là căn bậc n của số b nếu aⁿ = b.

> Chú ý:

+) Với n lẻ và b ∈ R thì có duy nhất một căn bậc n của b, kí hiệu $\small \sqrt[n]{b}$

+) Với n chẵn và:

b<0 thì không tồn tại căn bậc n của b.

b=0 thì có duy nhất một căn bậc n của b là số 0.

b) Tính chất của căn bậc n

- Từ định nghĩa ta có các tính chất sau:

$\small \sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}$

$\small \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$

$\small (\sqrt[n]{a})^m=\sqrt[n]{a^m}$

$\dpi{100} \small \sqrt[n]{a^n}=\left\{\begin{matrix} a,\: khi \: n\: ch\tilde{\check{a}}n\\|a|,\: khi \: n\: l\acute{e} \end{matrix}\right.$

$\small \sqrt[n]{{\sqrt[k]a}}=\sqrt[nk]{a}$

3. Lũy thừa với số mũ hữu tỉ

- Cho số thực a dương và số hữu tỉ $\small r=\frac{m}{n}$ , trong đó m∈Z, n∈N^*. Lũy thừa của số a với số mũ r là số a^r xác định bởi:

$\small a^r = a^{\frac{m}{n}} = \sqrt[n]{a^m}$

> Chú ý: $\small a^{\frac{1}{n}}=\sqrt[n]{a}$

* Ví dụ: $\small 27^{-\frac{4}{3}}=\sqrt[3]{27^{-4}}=\sqrt[3]{\frac{1}{27^4}}$ $\small =\frac{1}{\sqrt[3]{27^4}} = \frac{1}{(\sqrt[3]{27})^4}=\frac{1}{3^4}=\frac{1}{81}$

II. Tính chất của lũy thừa với số mũ thực

Cho a, b là những số thực dương; α, β là những số thực tùy ý. Khi đó ta có:

$\small a^\alpha .a^\beta =a^{\alpha +\beta }$

$\small \frac{a^\alpha}{a^\beta} =a^{\alpha -\beta }$

$\small (a^\alpha )^\beta =a^{\alpha \beta }$

$\small (ab)^\alpha =a^{\alpha }b^{\alpha }$

$\small \left ( \frac{a}{b} \right )^{\alpha }=\frac{a^\alpha }{b^\alpha }$

Nếu a>1 thì a^α > a^β ⇔ α > β.

Nếu a<1 thì a^α > a^β ⇔ α < β

III. Câu hỏi vận dụng

* Câu hỏi 1 trang 50 SGK Toán 12 Giải tích: Tính (1,5)⁴; ((-2)/3)³; (√3)⁵.

> Lời giải:

- Ta có: (1,5)⁴ = 5.0625; [(-2)/3]³=-8/27; (√3)⁵ = 9√3.

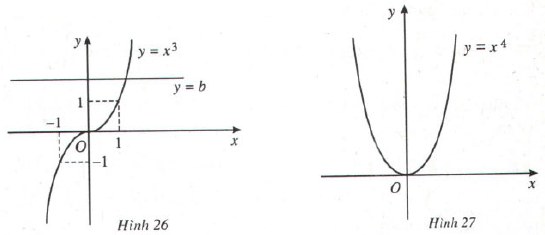
* Câu hỏi 2 trang 51 SGK Toán 12 Giải tích: Dựa vào đồ thị của các hàm số y = x³ và y = x⁴ (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình x³ = b và x⁴ = b.

Câu hỏi 2 trang 51 sgk toán 12 giải tích

> Lời giải:

° Số nghiệm của phương trình x³ = b là số giao điểm của hai đồ thị hàm số y = b và y = x³.

Dựa vào H.26 ta có đồ thị hàm số y = x³ luôn cắt đường thẳng y = b tại một điểm duy nhất với mọi b nên phương trình x³ = b luôn có nghiệm duy nhất với mọi b.

° Số nghiệm của phương trình x⁴ = b (1) là số giao điểm của hai đồ thị hàm số y = b và y = x⁴. Dựa và H.27 ta có:

- Với b < 0 hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.

- Với b = 0, hai đồ thị hàm số tiếp xúc nhau tại (0,0), vậy phương trình (1) có nghiệm duy nhất x = 0.

- Với b > 0, hai đồ thị hàm số cắt nhau tại hai điểm phân biệt, vậy phương trình (1) có hai nghiệm phân biệt.

* Câu hỏi 3 trang 53 SGK Toán 12 Giải tích: Chứng minh tính chất $\small \sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}$ .

> Lời giải:

- Đặt $\small \sqrt[n]{a}=x;\: \sqrt[n]{b}=y$ khi đó: xⁿ = a, yⁿ = b.

Ta có (xy)ⁿ = xⁿ.yⁿ = a.b.

Vậy xy là căn bậc n của ab.

Suy ra: $\small \sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}$

* Câu hỏi 4 trang 55 SGK Toán 12 Giải tích: Hãy nhắc lại các tính chất của lũy thừa với số mũ nguyên dương.

> Lời giải:

° Các tính chất về đẳng thức của lũy thừa với số mũ nguyên dương

1. a^m. aⁿ = a^(m+n)

2. a^m : aⁿ = a^(m-n) (m ≥ n).

3. (a^m)ⁿ = a^mn

4.(a/b)^m = a^m / b^m (b ≠ 0)

5. (ab)^m = a^m.b^m

° Các tính chất về bất đẳng thức của lũy thừa với số mũ nguyên dương

- Với a > 1 thì a^m > aⁿ ⇔ m > n.

- Với 0 < a < 1 thì a^m > aⁿ ⇔ m < n.

- Với 0 < a < b thì a^m > b^m

* Câu hỏi 5 trang 56 SGK Toán 12 Giải tích: Rút gọn biểu thức:

$\small \frac{(a^{\sqrt{3}-1})^{\sqrt{3}+1}}{a^{\sqrt{5}-3}.a^{4-\sqrt{5}}};\: (a>0)$

> Lời giải:

- Ta có: $\small \frac{(a^{\sqrt{3}-1})^{\sqrt{3}+1}}{a^{\sqrt{5}-3}.a^{4-\sqrt{5}}} =\frac{a^{(\sqrt{3}-1)(\sqrt{3}+1)}}{a^{(\sqrt{5-3+4-\sqrt{5}})}}$ $\small =\frac{a^{3-1}}{a^{1}}=\frac{a^2}{a}=a$

* Câu hỏi 6 trang 56 SGK Toán 12 Giải tích: So sánh các số $\small \left ( \frac{3}{4} \right )^{\sqrt{8}}$ và $\small \left ( \frac{3}{4} \right )^{3}$

> Lời giải:

- Ta có: $\small 0<\frac{3}{4}<1$ và $\small \sqrt{8}<3$ nên $\small \left ( \frac{3}{4} \right )^{\sqrt{8}}>\left ( \frac{3}{4} \right )^{3}$

Trên đây KhoiA.Vn đã giới thiệu với các em về Lũy thừa, tính chất của lũy thừa với số mũ thực, căn bậc n và tính chất căn bậc n. Hy vọng bài viết giúp các em hiểu rõ hơn. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết, chúc các em thành công.

Lũy thừa là gì? Tính chất của lũy thừa với số mũ thực, căn bậc n và tính chất căn bậc n - Toán 12 bài 1

Tags

Đánh giá & nhận xét