Bài tập Tìm Cực trị (Cực đại, Cực tiểu) của hàm số - Giải tích 12 bài 2

18:36:4418/07/2021

Nội dung lý thuyết về các tìm (quy tắc) tìm cực trị (cực đại, cực tiểu) của hàm số các em đã được tìm hiểu ở bài trước. Bài này chúng ta sẽ vận dụng giải một số bài tập tìm cực trị của hàm số.

Một số dạng bài tập cơ bản như tìm cực trị (cực đại, cực tiểu) áp dụng quy tắc I hoặc quy tắc II (với một số bài toán chúng ta có thể áp dụng bất kỳ 1 trong 2 cách để tìm cực trị); hay các bài toán chứng minh điểm cực đại, cực tiểu; tìm tham số m để hàm cực đại hay cực tiểu tại 1 điểm,... sẽ được giới thiệu trong bài viết này.

• Lý thuyết Cực trị của hàm số và 2 quy tắc tìm cực trị

* Bài 1 trang 18 SGK Giải tích 12: Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:

a) y = 2x³ + 3x² - 36x - 10

b) y = x⁴ + 2x² - 3

c) $\small y=x+\frac{1}{x}$

d) y = x³(1 - x)²

e) $\small y=\sqrt{x^2-x+1}$

> Lời giải:

a) y = 2x³ + 3x² - 36x - 10

- TXĐ: D = R

y' = 6x² + 6x - 36

y' = 0 ⇔ 6x² + 6x - 36 = 0

⇔ x² + x - 6x =0 ⇔ x -3 hoặc x = 2

- Bảng biến thiên: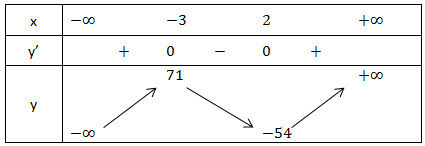 bảng biến thiên câu a

- Kết luận :

Hàm số đạt cực đại tại x = -3 ; y_CĐ = 71

Hàm số đạt cực tiểu tại x = 2; y_CT = -54.

b) y = x⁴ + 2x² - 3

- TXĐ: D = R

y'= 4x³ + 4x = 4x(x² + 1) = 0;

y' = 0 ⇔ 4x(x² + 1) = 0 ⇔ x = 0

- Bảng biến thiên: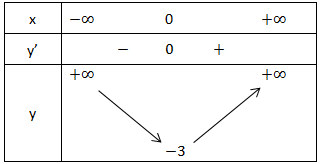 bảng biến thiên câu b

Vậy hàm số đạt cực tiểu tại x = 0; y_CT = -3

Hàm số không có điểm cực đại.

c) $\small y=x+\frac{1}{x}$

- TXĐ: D = R\{0}

$\small y'=1-\frac{1}{x^2}$ ; $\small y'=0\Leftrightarrow 1-\frac{1}{x^2}=0\Leftrightarrow x=\pm 1$

- Bảng biến thiên:

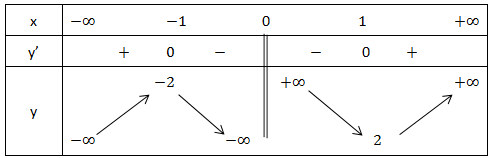
bảng biến thiên câu c

Vậy hàm số đạt cực đại tại x = -1; y_CĐ = -2;

Hàm số đạt cực tiểu tại x = 1; y_CT = 2.

d) y = x³(1 - x)²

- Ta có: y'= (x³)’.(1 – x)² + x³.[(1 – x)²]’

= 3x².(1 – x)² + x³.2(1 – x).(1 – x)’

= 3x²(1 – x)² - 2x³(1 – x)

= x².(1 – x)(3 – 5x)

y' = 0 ⇔ x = 0; x = 1 hoặc x = 3/5

- Bảng biến thiên: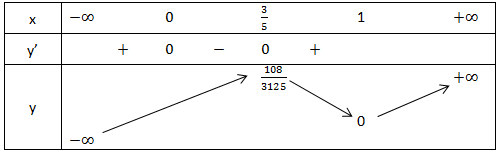

Vậy hàm số đạt cực đại tại x = 3/5 ; y_CĐ = 108/3125

Hàm số đạt cực tiểu tại x_CT = 1. y_CT = 0;

> Lưu ý: x = 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.

e) $\small y=\sqrt{x^2-x+1}$

- Ta có: TXĐ: D = R.

$\small y'=\frac{2x-1}{2\sqrt{x^2-x+1}}$

$\small y'=0\Leftrightarrow \frac{2x-1}{2\sqrt{x^2-x+1}}=0$ $\small \Leftrightarrow 2x-1=0\Leftrightarrow x=\frac{1}{2}$

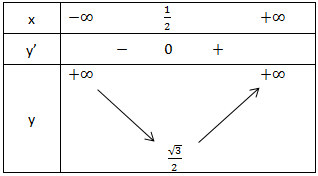
- Bảng biến thiên: bảng biến thiên câu e

Vậy hàm số đạt cực tiểu tại x = 1/2, y_CT = (√3)/2.

* Bài 2 trang 18 SGK Giải tích 12: Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:

a) y = x⁴ - 2x² + 1;

b) y = sin2x – x

c) y = sinx + cosx;

d) y = x⁵ - x³ - 2x + 1

> Lời giải:

a) y = x⁴ - 2x² + 1;

- TXĐ: D = R.

- Ta có: y' = 4x³ - 4x

y' = 0 ⇔ 4x(x² – 1) = 0 ⇔ x = 0 hoặc x = ±1.

- Lại có y" = 12x² - 4

y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.

y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.

y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.

b) y = sin2x – x

- TXĐ: D = R.

- Ta có: y' = 2cos2x – 1;

y' = 0 ⇔ 2cos2x - 1 = 0 ⇔ cos2x = 1/2

$\small \Leftrightarrow 2x=\pm \frac{\pi }{3}+k2\pi\: (k\in \mathbb{Z})$ $\small \Leftrightarrow x=\pm \frac{\pi }{6}+k\pi\: (k\in \mathbb{Z})$

- Lại có: y'' = -4sin2x

$\small y''\left (\frac{\pi }{6} +k\pi \right )=-4sin\left ( \frac{\pi }{3}+k2\pi \right )$ $\small =-2\sqrt{3}<0,\: (k\in \mathbb{Z})$

$\small \Rightarrow x=\frac{\pi }{6}+k\pi ,\: (k\in \mathbb{Z})$ là các điểm cực đại của hàm số.

$\small y''\left (-\frac{\pi }{6} +k\pi \right )=-4sin\left (- \frac{\pi }{3}+k2\pi \right )$ $\small =2\sqrt{3}<0,\: (k\in \mathbb{Z})$

$\small \Rightarrow x=-\frac{\pi }{6}+k\pi ,\: (k\in \mathbb{Z})$ là các điểm cực tiểu của hàm số.

c) y = sinx + cosx;

- TXĐ: D = R

- Ta có: y' = cosx - sinx

y' = 0 ⇔ cosx - sinx = 0

$\small \Leftrightarrow \sqrt{2}.cos\left ( x+\frac{\pi }{4} \right )=0$ $\small \Leftrightarrow x+\frac{\pi }{4}=\frac{\pi }{2}+k\pi ,\: (k\in \mathbb{Z})$

$\small \Leftrightarrow x=\frac{\pi }{4}+k\pi ,\: (k\in \mathbb{Z})$

- Lại có: $\small y'' = -sinx - cosx = \sqrt{2}.cos(x-\frac{\pi }{4})$

$\small y''\left ( \frac{\pi }{4}+k2\pi \right )=-\sqrt{2}.cos(k2\pi )=-\sqrt{2}<0$

$\small \Rightarrow x=\frac{\pi }{4}+k2\pi ,\: (k\in \mathbb{Z})$ là các điểm cực đại của hàm số.

$\small y''\left ( \frac{5\pi }{4}+k2\pi \right )=-\sqrt{2}.cos(\pi +k2\pi )=\sqrt{2}>0$

$\small \Rightarrow x=\frac{5\pi }{4}+k2\pi ,\: (k\in \mathbb{Z})$ là các điểm cực tiểu của hàm số.

d) y = x⁵ - x³ - 2x + 1

- TXĐ: D = R

- Ta có: y'= 5x⁴ - 3x² - 2

y' = 0 ⇔ 5x⁴ – 3x² – 2 = 0

⇔ x² = 1 ⇔ x = 1 hoặc x = -1.

- Lại có: y" = 20x³ - 6x

y"(-1) = -20 + 6 = -14 < 0

⇒ x = -1 là điểm cực đại của hàm số.

y"(1) = 20 – 6 = 14 > 0

⇒ x = 1 là điểm cực tiểu của hàm số.

* Bài 3 trang 18 SGK Giải tích 12: Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.

> Lời giải:

- Hàm số có tập xác định D = R và liên tục trên R.

- Chứng minh hàm số y = f(x) = √|x| không có đạo hàm tại x = 0.

$\small y=f(x)=\sqrt{|x|}=\left\{\begin{matrix} \sqrt{x}\:\: khi \: x\geq 0\\ \sqrt{-x}\: \: khi \: x\leq 0 \end{matrix}\right.$

- Ta có:

$\small \lim_{x\rightarrow 0^{+}}\frac{f(x)-f(0)}{x-0}$ $\small =\lim_{x\rightarrow 0^{+}}\frac{\sqrt{x}}{x}=\lim_{x\rightarrow 0^{+}}\frac{1}{\sqrt{x}}=+\infty \boldsymbol{}$

$\small \lim_{x\rightarrow 0^{-}}\frac{f(x)-f(0)}{x-0}$ $\small =\lim_{x\rightarrow 0^{-}}\frac{\sqrt{-x}}{x} =\lim_{x\rightarrow 0^{-}}\frac{\sqrt{-x}}{-(\sqrt{-x})^2}$ $\small =\lim_{x\rightarrow 0^{-}}\frac{-1}{\sqrt{-x}}=-\infty$

$\small \Rightarrow \small \lim_{x\rightarrow 0^{+}}\frac{f(x)-f(0)}{x-0}\neq \small \lim_{x\rightarrow 0^{-}}\frac{f(x)-f(0)}{x-0}$

$\Rightarrow$ ⇒ Nên không tồn tại giới hạn: $\lim_{x\rightarrow 0}\frac{f(x)-f(0)}{x-0}$

⇒ Không tồn tại đạo hàm của hàm số đã cho tại x = 0.

Dễ thấy $\small f(x)=\sqrt{|x|}\geq 0$ với mọi x ∈ R và f(0) = 0 nên x = 0 chính là điểm cực tiểu của hàm số.

* Bài 4 trang 18 SGK Giải tích 12: Chứng minh rằng với mọi giá trị của tham số m, hàm số:

y = x³ - mx² - 2x + 1

luôn luôn có một cực đại và một điểm cực tiểu.

> Lời giải:

- TXĐ: D = R

- Ta có: y' = 3x² - 2mx – 2

y' = 0 ⇔ 3x² – 2mx – 2 = 0 $\small \Leftrightarrow \left \[\begin{matrix} x=\frac{m-\sqrt{m^2+6}}{3}\\ x=\frac{m+\sqrt{m^2+6}}{3} \end{matrix} \right.$

- Lại có: y'' = 6x – 2m. nên:

$\small y''\left ( \frac{m-\sqrt{m^2+6}}{3} \right )=-2\sqrt{m^2+6}<0$

$\small \Rightarrow x=\frac{m-\sqrt{m^2+6}}{3}$ là một điểm cực đại của hàm số.

$\small y''\left ( \frac{m+\sqrt{m^2+6}}{3} \right )=2\sqrt{m^2+6}>0$

$\small \Rightarrow x=\frac{m+\sqrt{m^2+6}}{3}$ là một điểm cực tiểu của hàm số.

- Vậy với mọi giá trị tham số của m thì hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.

- Nhận xét: Thực ra, với yêu cầu của bài toán này thì chúng ta chỉ cần tính Δ' = m² - 6 > 0 với mọi giá trị của m, nên y' luôn có 2 nghiệm phân biệt và y' đổi dấu khi qua các nghiệm đó. (hàm đa thức bậc 3 có 1 điểm cực đại và 1 điểm cực tiểu khi và chỉ khi y'=0 có 2 nghiệm phân biệt).

* Bài 5 trang 18 SGK Giải tích 12: Tìm a và b để các cực trị của hàm số:

$\small y=\frac{5}{3}a^2x^3+2ax^2-9x+b$

đều là những số dương và x_o = -5/9 là điểm cực đại.

> Lời giải:

- TXĐ: D = R.

- Ta có: y' = 5a²x² + 4ax – 9.

⇒ y'' = 10a²x + 4a.

• Nếu a = 0 thì y' = -9 < 0 với ∀ x ∈ R

⇒ Hàm số không có cực trị (loại)

• Nếu a ≠ 0.

y' = 0 ⇔ 5a²x² + 4ax – 9 = 0

⇔ 5(ax)² + 4(ax) – 9 = 0

$\small \Leftrightarrow \left \[\begin{matrix} ax=1\\ ax=-\frac{9}{5} \end{matrix} \right. \Leftrightarrow \left \[\begin{matrix} x=\frac{1}{a}\\ \\ x=-\frac{9}{5a} \end{matrix} \right.$

Khi đó, ta có:

$\small y''\left ( \frac{1}{a} \right )=14a;\: \: y''\left ( \frac{-9}{5a} \right )=-14a$

¤ TH1: x = 1/a là điểm cực đại (điểm này phải trùng x₀ bài cho), khi đó

$\small \left\{\begin{matrix} \frac{1}{a}=-\frac{5}{9}\\ 14a<0 \end{matrix}\right.\Leftrightarrow a=\frac{-9}{5}$ khi đó: $\small y_{CD}=f\left ( \frac{1}{a} \right )=\frac{80}{27}+b$

⇒ x = (-9)/5a là điểm cực tiểu, khi đó: $\small y_{CT}=f\left ( \frac{-9}{5a}\right )=\frac{-36}{5}+b$

- Các cực trị của hàm số đều dương: $\small \left\{\begin{matrix} \frac{80}{27}+b>0\\ \\ \frac{-36}{5}+b>0 \end{matrix}\right.\Leftrightarrow b>\frac{36}{5}$

¤ TH2: x =(-9)/5a là điểm cực đại (điểm này phải trùng x₀ bài cho), khi đó:

$\small \left\{\begin{matrix} \frac{-9}{5a}=\frac{-5}{9}\\ -14a<0 \end{matrix}\right.\Leftrightarrow a=\frac{81}{25}$ khi đó: $\small y_{CD}=f\left ( \frac{-9}{5a} \right )=4+b$

⇒ x = 1/a là điểm cực tiểu, khi đó $\small y_{CT}=f\left ( \frac{1}{a} \right )=\frac{-400}{243}+b$

- Các cực trị của hàm số đều dương: $\small \left\{\begin{matrix} 4+b>0\\ \\ \frac{-400}{243}+b>0 \end{matrix}\right. \Leftrightarrow b>\frac{400}{243}$

Kết luận: $\small \left\{\begin{matrix} a=\frac{-9}{5}\\ \\b>\frac{36}{5} \end{matrix}\right.$ hoặc $\small \left\{\begin{matrix} a=\frac{81}{5}\\ \\b>\frac{400}{243} \end{matrix}\right.$ là các giá trị cần tìm.

* Bài 6 trang 18 SGK Giải tích 12: Xác định giá trị của tham số m để hàm số m để hàm số $\small y=\frac{x^2+mx+1}{x+m}$ đạt giá trị cực đại tại x = 2.

> Lời giải:

- TXĐ: D = R{-m}

- Ta có: $\small y=x+\frac{1}{x+m}\Rightarrow y'=1-\frac{1}{(x+m)^2}$

- Lại có: $\small y''=\frac{2(x+m)}{(x+m)^4}=\frac{2}{(x+m)^3}$

Hàm số đạt cực đại tại $\small x=2\Leftrightarrow \left\{\begin{matrix} y'(2)=0\\ y''(2)<0 \end{matrix}\right.$

- Có: $\small y'(2)=0\Leftrightarrow 1-\frac{1}{(2+m)^2}=0$

$\small \Leftrightarrow (m+2)^2=1\Leftrightarrow \left \[\begin{matrix} m=-1\\ m=-3 \end{matrix} \right.$ (1)

- Có $\small y''(2)<0\Leftrightarrow \frac{2}{(2+m)^3}<0$

$\small (2+m)^3<0\Leftrightarrow 2+m<0 \Leftrightarrow m<-2$ (2)

Kết hợp (1) và (2) ta suy ra m = -3 (thỏa).

Vậy m=-3 thì hàm số đạt cực đại tại x = 2.

Trên đây là bài viết hướng dẫn giải một số bài tập về tìm cực trị (cực đại, cực tiểu) của hàm số với một số dạng vận dụng tìm cực trị với quy tắc I hoặc quy tắc II hay các bài toán chứng minh điểm cực đại, cực tiểu; tìm tham số m để hàm cực đại hay cực tiểu tại 1 điểm,... KhoiA hy vọng các em hiểu rõ và vận dụng tốt vào các bài tập tìm cực trị.

Bài tập Tìm Cực trị (Cực đại, Cực tiểu) của hàm số - Giải tích 12 bài 2

Tags

Đánh giá & nhận xét