Các dạng bài tập về bất phương trình mũ và cách giải - Toán lớp 12

15:20:5019/11/2020

Khi học tới bất phương trình mũ thì các em đã biết các phương pháp giải phương trình mũ. Bất phương trình nhìn chung sẽ ở một mức khó hơn đối với đa số các em, vì vậy, nội dung bất phương trình mũ sẽ có nhiều bài tập khó nhằn hơn.

Vậy bất phương trình mũ có những dạng bài tập nào? cách giải các dạng bài tập bất phương trình mũ như thế nào? Bài viết này, chúng ta cùng đi hệ thống lại các dạng bài tập về bất phương trình mũ thường gặp. Qua đó rèn luyện kỹ năng giải toán bất phương trình mũ qua các bài tập và ví dụ minh họa.

I. Các dạng bài tập bất phương trình Mũ

° Dạng 1: Bất phương trình mũ có dạng a^f(x) ≤ a^g(x)

* Phương pháp giải:

- Để giải bất phương trình mũ dạng này ta sử dụng phép biến đổi tương đương như sau:

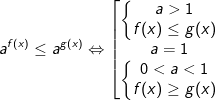$a^{f(x)}\leq a^{g(x)}\Leftrightarrow \left \[\begin{matrix} \left\{\begin{matrix} a>1\\ f(x)\leq g(x) \end{matrix}\right.\\ a=1\\ \left\{\begin{matrix} 0<a<1\\ f(x)\geq g(x) \end{matrix}\right. \end{matrix} \right.$ hoặc $\left\{\begin{matrix} a>0\\ (a-1)[f(x)-g(x)]\leq 0 \end{matrix}\right.$

* Ví dụ 1: Giải bất phương trình mũ sau: 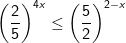$\left ( \frac{2}{5} \right )^{4x}\leq \left ( \frac{5}{2} \right )^{2-x}$

* Lời giải:

- Ta có thể biến đổi theo 1 trong 2 cách sau (thực tế thì cùng phương pháp):

+ Cách 1: Bất phương trình được biến đổi về dạng:

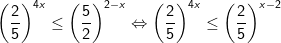
$\left ( \frac{2}{5} \right )^{4x}\leq \left ( \frac{5}{2} \right )^{2-x}\Leftrightarrow \left ( \frac{2}{5} \right )^{4x}\leq \left ( \frac{2}{5} \right )^{x-2}$

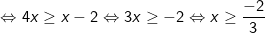
$\Leftrightarrow 4x\geq x-2\Leftrightarrow 3x\geq -2\Leftrightarrow x\geq \frac{-2}{3}$

Vậy tập nghiệm của bất phương trình là: 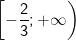$\left [ -\frac{2}{3};+\infty \right )$

+ Cách 2: Bất phương trình được biến đổi về dạng:

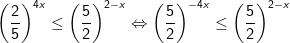
$\left ( \frac{2}{5} \right )^{4x}\leq \left ( \frac{5}{2} \right )^{2-x}\Leftrightarrow \left ( \frac{5}{2} \right )^{-4x}\leq \left ( \frac{5}{2} \right )^{2-x}$

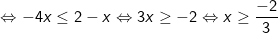
$\Leftrightarrow -4x\leq 2-x\Leftrightarrow 3x\geq -2\Leftrightarrow x\geq \frac{-2}{3}$

Kết luận: Tập nghiệm của bất phương trình mũ là: S=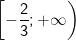 $\left [ -\frac{2}{3};+\infty \right )$

> Nhận xét: Trong hai cách biến đổi ở trên ta cùng một mục đích là đưa phương trình đã có về dạng có cùng cơ số.

- Trong cách 1: với việc sử dụng cơ số a<1 nên dấu bất đẳng thức phải đổi chiều, vì vậy mà các em cần chú ý vì nhiều bạn hay sai ở phép biến đổi này.

- Trong cách 2: Với việc sử dụng cơ số a>1 nên dấu bất đẳng thức không đổi chiều, vì vậy các em có thể sử dụng cách 2 này để tránh sai sót ở các bài toán tương tự.

* Ví dụ 2: Giải bất phương trình mũ sau: 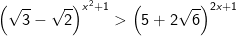$\left ( \sqrt{3}-\sqrt{2} \right )^{x^2+1}>\left ( 5+2\sqrt{6} \right )^{2x+1}$

* Lời giải:

- Ta có thể biến đổi theo 1 trong 2 cách sau:

+ Cách 1:

- Ta thấy: 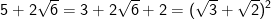$5+2\sqrt{6}=3+2\sqrt{6}+2=(\sqrt{3}+\sqrt{2})^2$

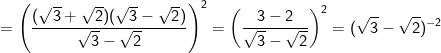
$=\left ( \frac{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}{\sqrt{3}-\sqrt{2}} \right )^2=\left ( \frac{3-2}{\sqrt{3}-\sqrt{2}} \right )^2=(\sqrt{3}-\sqrt{2})^{-2}$

- Do đó, bất phương trình được biến đổi như sau:

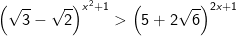
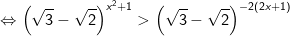
$\left ( \sqrt{3}-\sqrt{2} \right )^{x^2+1}>\left ( 5+2\sqrt{6} \right )^{2x+1}$ $\Leftrightarrow \left ( \sqrt{3}-\sqrt{2} \right )^{x^2+1}>\left (\sqrt{3}-\sqrt{2} \right )^{-2(2x+1)}$

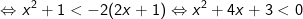
$\Leftrightarrow x^2+1<-2(2x+1)\Leftrightarrow x^2+4x+3<0$

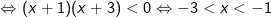
$\Leftrightarrow (x+1)(x+3)<0\Leftrightarrow -3<x<-1$

Vậy tập nghiệm của bất phương trình là (-3;-1)

+ Cách 2:

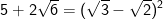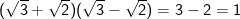
- Ta thấy: $5+2\sqrt{6}=(\sqrt{3}-\sqrt{2})^2$ mà $(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})=3-2=1$

nên suy ra: 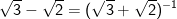$\sqrt{3}-\sqrt{2}=(\sqrt{3}+\sqrt{2})^{-1}$

- Do đó, bất phương trình được biến đổi như sau:

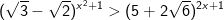
$(\sqrt{3}-\sqrt{2})^{x^2+1}>(5+2\sqrt{6})^{2x+1}$

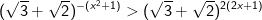
$(\sqrt{3}+\sqrt{2})^{-(x^2+1)}>(\sqrt{3}+\sqrt{2})^{2(2x+1)}$

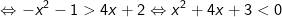
$\Leftrightarrow -x^2-1>4x+2\Leftrightarrow x^2+4x+3<0$

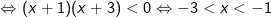
$\Leftrightarrow (x+1)(x+3)<0\Leftrightarrow -3<x<-1$

Kết luận: Tập nghiệm của bất phương trình mũ là:S=(-3;-1)

> Nhận xét: Trong hai cách biến đổi ở trên ta cùng một mục đích là đưa phương trình đã có về dạng có cùng cơ số.

- Trong cách 1: Với việc biến đổi đưa vế phải về cùng cơ số với vế trái, khi đó, cơ số a<1 nên dấu bất đẳng thức phải đổi chiều, vì vậy mà các em cần chú ý vì nhiều bạn hay sai ở phép biến đổi này.

- Trong cách 2: Với việc biến đổi đưa vế trái và vế phải về cùng 1 cơ số trung gian (có cơ số a>1) nên dấu bất đẳng thức không đổi chiều, vì vậy các em có thể sử dụng cách 2 này để tránh sai sót ở các bài toán tương tự.

° Dạng 2: Bất phương trình mũ có dạng a^f(x) < b (b>0).

* Phương pháp giải:

- Để giải bất phương trình mũ dạng này ta sử dụng phép biến đổi tương đương như sau:

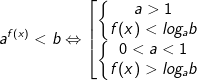
$a^{f(x)}<b\Leftrightarrow \left \[\begin{matrix} \left\{\begin{matrix} a>1\\ f(x)<log_ab \end{matrix}\right.\\ \left\{\begin{matrix} 0<a<1\\ f(x)>log_ab \end{matrix}\right. \end{matrix} \right.$

* Ví dụ: Giải bất phương trình mũ sau: 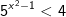$5^{x^2-1}<4$

* Lời giải:

- Bất phương trình biến đổi về dạng sau:

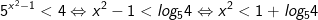
$5^{x^2-1}<4\Leftrightarrow x^2-1<log_54\Leftrightarrow x^2<1+log_54$

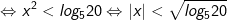
$\Leftrightarrow x^2<log_520\Leftrightarrow |x|<\sqrt{log_520}$

Kết luận: Tập nghiệm của bất phương trình là:S= $(-\sqrt{log_520};\sqrt{log_520})$

° Dạng 3: Bất phương trình mũ có dạng a^f(x) > b.

* Phương pháp giải:

- Để giải bất phương trình mũ dạng này ta sử dụng phép biến đổi tương đương như sau:

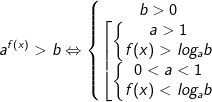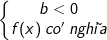
$a^{f(x)}>b\Leftrightarrow \left\{\begin{matrix} b>0\\ \left \[\begin{matrix} \left\{\begin{matrix} a>1\\ f(x)>log_ab \end{matrix}\right.\\ \left\{\begin{matrix} 0<a<1\\ f(x)<log_ab \end{matrix}\right. \end{matrix} \right. \end{matrix}\right.$ hoặc $\left\{\begin{matrix} b<0\\ f(x)\: {co}'\: nghi\tilde{}a \end{matrix}\right.$

* Ví dụ: Giải bất phương trình mũ sau: 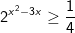$2^{x^2-3x}\geq \frac{1}{4}$

* Lời giải:

- Ta có:

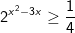
$2^{x^2-3x}\geq \frac{1}{4}$ $\Leftrightarrow 2^{(x^2-3x)}\geq 2^{-2}$

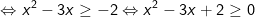
$\Leftrightarrow x^2-3x\geq -2\Leftrightarrow x^2-3x+2\geq 0$

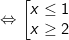
$\Leftrightarrow \left \[\begin{matrix} x\leq 1\\ x\geq 2 \end{matrix} \right.$

Kết luận: Vậy tập nghiệm của bất phương trình mũ là:S=(-∞; 1] ∪ [2; +∞)

II. Giải bất phương trình mũ và bất phương trình logarit bằng phương pháp đặt ẩn phụ

- Các dạng đặt ẩn phụ trong trường hợp này cũng giống như với phương trình mũ và phương trình logarit.

* Ví dụ: Giải bất phương trình mũ sau:

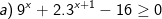
$a)\: 9^x+2.3^{x+1}-16\geq 0$

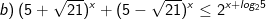
$b)\: (5+\sqrt{21})^x+(5-\sqrt{21})^x\leq 2^{x+log_25}$

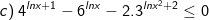
$c)\: 4^{lnx+1}-6^{lnx}-2.3^{lnx^2+2}\leq 0$

* Lời giải:

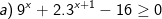$a)\: 9^x+2.3^{x+1}-16\geq 0$ (*)

- Ta đặt t = 3^x (điều kiện t>0), khi đó phương trình (*) biến đổi về dạng:

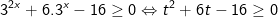
$3^{2x}+6.3^x-16\geq 0\Leftrightarrow t^2+6t-16\geq 0$

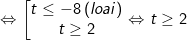
$\Leftrightarrow \left \[\begin{matrix} t\leq -8\: (loai)\\ t\geq 2 \end{matrix} \right.\Leftrightarrow t\geq 2$

Với: 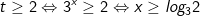$t\geq 2\Leftrightarrow 3^x\geq 2\Leftrightarrow x\geq log_32$

Vậy bất phương trình có tập nghiệm (log₃2;+∞).

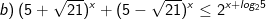
$b)\: (5+\sqrt{21})^x+(5-\sqrt{21})^x\leq 2^{x+log_25}$

- Chia 2 vế của bất phương trình cho 2^x, ta được:

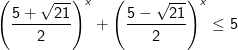$\left (\frac{5+\sqrt{21}}{2} \right )^x+\left (\frac{5-\sqrt{21}}{2} \right )^x\leq 5$ (*)

- Mặt khác, ta thấy: 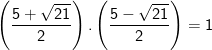$\left (\frac{5+\sqrt{21}}{2} \right ).\left (\frac{5-\sqrt{21}}{2} \right )=1$

Nêu nếu đặt 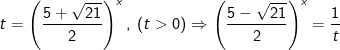$t=\left (\frac{5+\sqrt{21}}{2} \right )^x,\: (t> 0)\Rightarrow \left (\frac{5-\sqrt{21}}{2} \right )^x=\frac{1}{t}$

Khi đó, bất phương trình (*) tương đương: 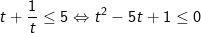$t+\frac{1}{t}\leq 5\Leftrightarrow t^2-5t+1\leq 0$

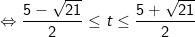
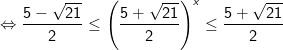
$\Leftrightarrow \frac{5-\sqrt{21}}{2}\leq t\leq \frac{5+\sqrt{21}}{2}$ $\Leftrightarrow\frac{5-\sqrt{21}}{2}\leq\left ( \frac{5+\sqrt{21}}{2} \right )^x \leq \frac{5+\sqrt{21}}{2}$

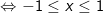
$\Leftrightarrow -1\leq x\leq 1$

Vậy tập nghiệm của bất phương trình là [-1;1]

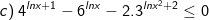
$c)\: 4^{lnx+1}-6^{lnx}-2.3^{lnx^2+2}\leq 0$

- Điều kiện: x>0

- Biến đổi bất phương trình về dạng: 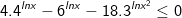$4.4^{lnx}-6^{lnx}-18.3^{lnx^{2}}\leq 0$ (*)

- Chia 2 vế của (*) cho 3^2lnx > 0 ta được: 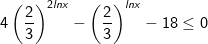$4\left ( \frac{2}{3} \right )^{2lnx}-\left ( \frac{2}{3} \right )^{lnx}-18\leq 0$

- Ta đặt $t=\left ( \frac{2}{3} \right )^{lnx$ điều kiện t > 0. Bất phương trình được đưa về dạng

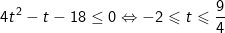$4t^2-t-18\leq 0\Leftrightarrow -2\leqslant t\leqslant \frac{9}{4}$ kết hợp điều kiện t>0 ta được

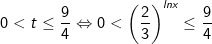
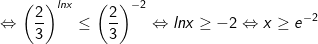
$0<t\leq \frac{9}{4}\Leftrightarrow 0< \left ( \frac{2}{3} \right )^{lnx}\leq \frac{9}{4}$ $\Leftrightarrow \left ( \frac{2}{3} \right )^{lnx}\leq \left ( \frac{2}{3} \right )^{-2}\Leftrightarrow lnx\geq -2\Leftrightarrow x\geq e^{-2}$

Vậy bất phương trình có tập nghiệm là: [e^-2;+∞)

Tóm lại, với 3 dạng bài tập cơ bản trên về bất phương trình mũ và cách giải cụ thể của các dạng này, KhoiA.Vn hy vọng giúp các em hiểu rõ hơn. Và về cơ bản, các em có thể giải quyết được nhiều bài toán bất phương trình mũ khi gặp trong đề thi tốt nghiệp THPT quốc gia. Chúc các em nhiều thành công

Các dạng bài tập về bất phương trình mũ và cách giải - Toán lớp 12

Tags

Đánh giá & nhận xét