Bài 7.42 trang 65 Toán 11 Kết nối tri thức Tập 2

Bài 7.42 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a, AA' ⊥ (ABCD) và  = 60^o.

a) Tính thể tích của khối hộp ABCD.A'B'C'D'.

b) Tính khoảng cách từ A đến mặt phẳng (A'BD).

Giải bài 7.42 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình vẽ sau:

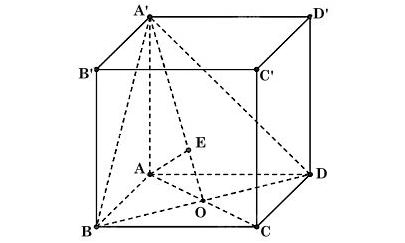
a) Gọi O là giao điểm của AC và BD.

Vì hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a nên ABCD là hình thoi,

⇒ AO = OC và AC  ⊥ BD.

Có S_ABD = .AO.BD = .CO.BD = S_BCD.

Nên S_ABCD = 2S_ABD.

Mà S_ABD = .AB.AD.sin = .a.a.sin60^o =  .

⇒ S_ABCD = 

Vậy, ta có:

b) Vì AO ⊥ BD mà AA' ⊥ (ABCD) nên AA' ⊥ BD.

Do đó BD ⊥ (AOA').

⇒ (A'BD) ⊥ (AOA').

Kẻ AE ⊥ A'O tại E. Vì (A'BD) ⊥ (AOA'), (A'BD) $\cap$ (AOA') = A'O và AE ⊥ A'O nên AE ⊥ (A'BD).

Do đó d(A, (A'BD)) = AE.

Xét tam giác ABD có AB = AD = a nên tam giác ABD là tam giác cân tại A

mà nên tam giác ABD đều,

⇒ BD = a

mà 

Xét tam giác AOB vuông tại O, có:

Vì AA' ⊥ (ABCD) nên AA' ⊥ AO hay tam giác A'AO vuông tại A.

Xét Δ A'AO vuông tại A có:

Vậy