Bài 7.39 trang 65 Toán 11 Kết nối tri thức Tập 2

Bài 7.39 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC.

a) Chứng minh rằng BC ⊥ (AID).

b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng AH ⊥ (BCD).

c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.

Giải bài 7.39 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình vẽ sau:

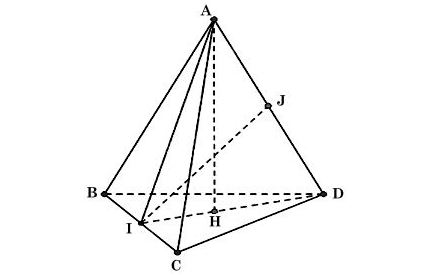
a) Vì tam giác ABC cân tại A, AI là trung tuyến nên AI đồng thời là đường cao hay AI ⊥ BC.

Vì tam giác BCD cân tại D, DI là trung tuyến nên DI đồng thời là đường cao hay DI ⊥ BC.

Có AI ⊥ BC và DI ⊥ BC

⇒ BC ⊥ (AID) (đpcm)

b) Do AH là đường cao của tam giác AID nên AH ⊥ DI.

Vì BC ⊥ (AID) nên BC ⊥ AH mà AH ⊥ DI

⇒ AH ⊥ (BCD) (đpcm)

c) Vì BC ⊥ (AID) nên BC ⊥ IJ, mà IJ là đường cao của tam giác AID nên IJ ⊥ AD.

⇒ IJ là đường vuông góc chung của AD và BC (đpcm)