Bài 7.40 trang 65 Toán 11 Kết nối tri thức Tập 2

Bài 7.40 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a và ∠CAB = 30^o. Biết SA ⊥ (ABC) và SA = a

a) Chứng minh rằng (SBC) ⊥ (SAB).

b) Tính theo a khoảng cách từ điểm A đến đường thẳng SC và khoảng cách từ điểm A đến mặt phẳng (SBC).

Giải bài 7.40 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình vẽ sau:

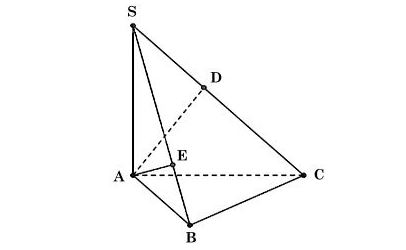
a) Do tam giác ABC vuông tại B nên AB ⊥ BC.

Vì SA ⊥ (ABC) nên SA ⊥ BC mà AB ⊥ BC nên BC ⊥ (SAB),

⇒ (SBC) ⊥ (SAB) (đpcm)

b) Kẻ AD ⊥ SC tại D. Khi đó d(A, SC) = AD.

Vì SA ⊥ (ABC) nên SA ⊥ AC nên tam giác SAC vuông tại A.

Xét ΔABC vuông tại B, có:

Xét ΔSAC vuông tại A, AD là đường cao, có:

Vậy 

Kẻ AE ⊥ SB tại E.

Vì BC ⊥ (SAB) nên BC ⊥ AE mà AE ⊥ SB nên AE ⊥ (SBC).

Khi đó d(A, (SBC)) = AE.

Xét tam giác ABC vuông tại B, có:

Vì SA ⊥ (ABC) nên SA ⊥ AB,

⇒ ΔSAB vuông tại A.

Xét ΔSAB vuông tại A, AE là đường cao, có: 

Vậy