Bài 7.37 trang 59 Toán 10 Kết nối tri thức Tập 2

Bài 7.37 trang 59 Toán 10 Tập 2 Kết nối tri thức:

Một cột trụ hình hypebol (H.7.36), có chiều cao 6 m, chỗ nhỏ nhất ở chính giữa và rộng 0,8 m, đỉnh cột và đáy cột đều rộng 1 m. Tính độ rộng của cột ở độ cao 5 m (tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).

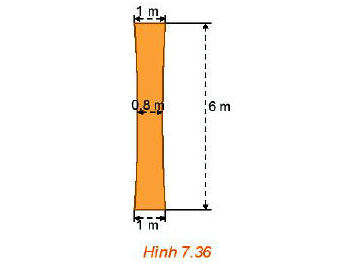
Giải bài 7.37 trang 59 Toán 10 Tập 2 Kết nối tri thức:

Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với điểm chính giữa hai cột, trục Oy đi qua điểm chính giữa, hai bên cột lần lượt nằm về hai phía của trục tung (như hình vẽ).

Phương trình hypebol (H) có dạng:  (với a, b > 0). 

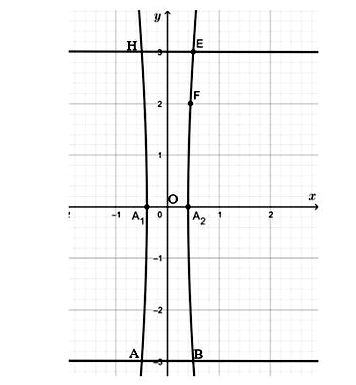
Theo bài ra ta có: A₁A₂ = 0,8 m; AB = EH = 1 m.

Khoảng cách giữa HE và AB là 6 m.

(H) cắt trục hoành tại hai điểm A₁, A₂, ta xác định được tọa độ 2 điểm là: A₁(− 0,4; 0) và A₂(0,4; 0).

Thay tọa độ A₂ vào phương trình (H) ta được: 

⇒ a = 0,4 (do a > 0).

Ta xác định được tọa độ điểm E là E(0,5; 3). 

(H) đi qua điểm có tọa độ E(0,5; 3) nên: 

. 

⇔ b² = 16 ⇒ b = 4 (vì b > 0).

Vậy phương trình (H) là:

Gọi F là điểm thuộc hypebol mà cột có độ cao 5 m. Ở độ cao 5 m thì khoảng cách từ vị trí F đó đến trục hoành là 2 m, tương ứng ta có tung độ điểm F là y = 2, ta cần tìm hoành độ của F. 

Thay y = 2 vào phương trình (H) ta có: 

⇔ x² = 0,2 ⇔ x ≈ ± 0,45. 

Vậy độ rộng của cột là: 0,45 . 2 = 0,9 m (độ rộng là khoảng cách nên phải dương).