Bài 5.6 trang 109 SGK Toán 11 tập 1 Kết nối tri thức

Bài 5.6 trang 109 Toán 11 tập 1 Kết nối tri thức:

Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA₁ ⊥ BC, từ A₁ kẻ A₁A₂ ⊥ AC, sau đó lại kẻ A₂A₃ ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA₁A₂A₃... Tính độ dài đường gấp khúc này theo h và α.

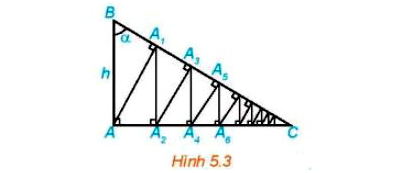
Giải bài 5.6 trang 109 Toán 11 tập 1 Kết nối tri thức:

• Tam giác AA₁B vuông tại A₁ có AB = h

Vì vậy: AA₁ = AB sinB = h.sinα.

Ta có:  và 

• Tam giác AA₁A₂ vuông tại A₂ nên A₁A₂ = AA₁ sin = h.sinα.sinα = h.sin²α.

Vì AB ⊥ AC và A₁A₂ ⊥ AC nên AB // A₁A₂, suy ra  (2 góc đồng vị).

• Tam giác A₁A₂A₃ vuông tại A₃ nên A₂A₃ = A­₁A₂ . sin = h.sin²α.sinα = h.sin³α.

 Vì AA₁ ⊥ BC và A₂A₃ ⊥ BC nên AA₁ // A₂A₃, suy ra 

• Tam giác A₂A₃A₄ vuông tại A₄ nên A₃A₄ = A₂A₃ . sin = h.sin³α.sinα = h.sin⁴α.

Cứ tiếp tục như vậy, ta xác định được A_{n – 1}A_n = h.sinⁿα.

Ta có: AA₁A₂A₃... = AA₁ + A₁A₂ + A₂A₃ + ... + A_{n – 1}A_n + ...

= h sin α + h sin² α + h sin³ α + ... + h sinⁿ α + ...

Vì góc B là góc nhọn nên sin B = sin α < 1, do đó |sin α| < 1.

Khi đó, độ dài của đường gấp khúc vô hạn AA₁A₂A₃... là tổng của cấp số nhân lùi vô hạn với số hạng đầu u₁ = h sin α và công bội q = sin α.

Nên có: