Bài 2.14 trang 32 SGK Toán 10 tập 1 Kết nối tri thức

Bài 2.14 trang 32 SGK Toán 10 Tập 1 Kết nối tri thức: 

Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ.

Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = –x – y với (x; y) thỏa mãn hệ trên.

Giải bài 2.14 trang 32 SGK Toán 10 Tập 1 Kết nối tri thức:

• Xác định miền nghiệm D₁ của bất phương trình y – 2x ≤ 2 được xác định như sau:

- Vẽ đường thẳng d₁ : –2x + y = 2.

- Ta lấy gốc tọa độ O(0;0) thay vào d₁ được: -2.0 + 0 = 0 < 2. Nên điểm O nằm trong miền nghiệm của bất phương trình.

Nên miền nghiệm D₁ là nửa mặt phẳng có bờ là đường thẳng d (bao gồm cả d₁) chứa gốc tọa độ.

• Miền nghiệm D₂ của bất phương trình y ≤ 4 là nửa mặt phẳng có bờ là đường thẳng d₂: y = 4 chứa gốc tọa độ.

• Miền nghiệm D₃ của bất phương trình x ≤ 5 là nửa mặt phẳng có bờ là đường thẳng d₃: x = 5 chứa gốc tọa độ.

• Xác định miền nghiệm D₄ của bất phương trình x + y ≥ –1 được xác định như sau:

- Vẽ đường thẳng d₄ : x + y = –1.

- Ta lấy gốc tọa độ O(0;0) thay vào d₄ được: 0 + 0 = 0 > –1. Nên điểm O nằm trong miền nghiệm của bất phương trình.

Nên miền nghiệm D₄ là nửa mặt phẳng có bờ là đường thẳng d₄ (bao gồm cả d₄) chứa gốc tọa độ.

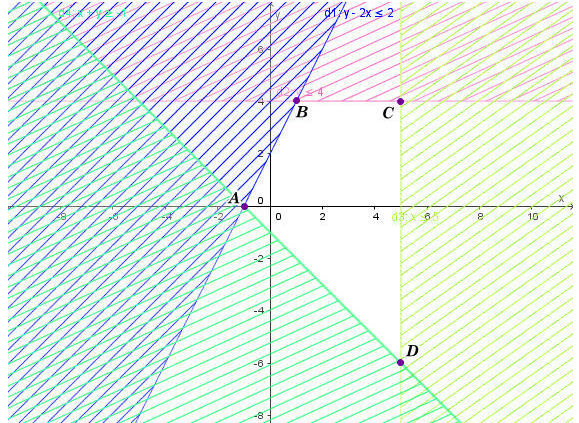
Khi đó miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với tọa độ các điểm là: A(–1; 0), B(1; 4), C(5; 4), D(5; –6) như hình trên.

Tính giá trị biểu thức F(x; y) = –x – y tại các điểm A, B, C, D

F(–1; 0) = –(–1) – 0 = 1;

F(1; 4) = –1 – 4 = –5;

F(5; 4) = –5 – 4 = –9;

F(5; –6) = –5 – (–6) = 1.

Vậy giá trị lớn nhất của biểu thức F = 1 tại (x; y) = (–1;0) hoặc (x;y) = (5; –6)

Và giá trị nhỏ nhất của biểu thức F = –9 tại (x; y) = (5;4)