Bài tập phép trừ hai số tự nhiên, phép chia hết và phép chia có dư - Toán 6 bài 6 tập 1 chương 1
Các em đã được biết nội dung lý thuyết về phép trừ hai số tự nhiên, phép chia hết và phép chia có dư của hai số tự nhiên qua bài viết trước.
Bài này sẽ chúng ta sẽ vận dụng kiến thức lý thuyết để giải một số bài tập về phép trừ hai số tự nhiên, phép chia hết và phép chia có dư của hai số tự nhiên.
• Lý thuyết phép trừ hai số tự nhiên, phép chia hết và phép chia có dư
Một số dạng bài tập cơ bản như: Thực hiện phép trừ, phép chia hai số tự nhiên; Vận dụng tính chất các phép tính để tính nhanh; và tìm số chưa biết trong một đẳng thức (tìm x).
* Bài 41 trang 22 SGK Toán 6 Tập 1: Hà Nội, Huế, Nha Trang, Thành phố Hồ Chí Minh nằm trên quốc lộ 1 theo thứ tự như trên. Cho biết các quãng đường trên quốc lộ ấy:
Hà Nội - Huế là 658 km
Hà Nội - Nha Trang là 1278 km
Hà Nội - Thành phố Hồ Chí Minh là 1710 km
Tính các quãng đường Huế - Nha Trang, Nha Trang – Thành phố Hồ Chí Minh.
> Lời giải:
- Ta có sơ đồ sau: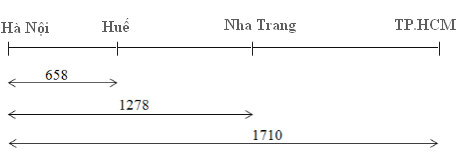
- Dựa vào sơ đồ trên ta dễ dàng tính được:
Quãng đường Huế – Nha Trang là:1278 – 658 = 620 (km)
Quãng đường Nha Trang – Thành phố Hồ Chí Minh là: 1710 – 1278 = 432 (km).
* Bài 42 trang 23 SGK Toán 6 Tập 1: Các số liệu về kênh đào Xuy–ê (Ai Cập) nối Địa Trung Hải và Hồng Hải được cho trong bảng 1 và bảng 2.
a) Trong bảng 1, các số liệu ở năm 1955 tăng thêm (hay giảm bớt) bao nhiêu so với năm 1869 (năm khánh thành kênh đào)?
b) Nhờ đi qua kênh đào Xuy–ê mỗi hành trình trong bảng 2 giảm bớt được bao nhiêu kilômét?
Bảng 1
| Kênh đào Xuy–ê | Năm 1869 | Năm 1955 |
| Chiều rộng mặt kênh | 58m | 135m |
| Chiều rộng đáy kênh | 22m | 50m |
| Độ sau của kênh | 6m | 13m |
| Thời gian tàu qua kênh | 48 giờ | 14 giờ |
Bảng 2
| Hành trình | Qua mũi Hảo Vọng | Qua kênh Xuy–ê |
| Luân Đôn – Bom–bay | 17400km | 10100km |
| Mác–xây – Bom-bay | 16000km | 7400km |
| Ô–đét-xa – Bom–bay | 19000km | 6800km |
> Lời giải:
a) Trong bảng 1: Số liệu năm 1955 so với năm 1869
Chiều rộng mặt kênh tăng: 135 – 58 = 77 (m)
Chiều rộng đáy kênh tăng: 50 – 22 = 28 (m)
Độ sâu của kênh tăng: 13 – 6 = 7 (m)
Thời gian tàu qua kênh giảm: 48 – 14 =34 (giờ)
b) Hành trình khi đi qua kênh đào Xuy–ê so với đi qua Mũi Hảo Vọng:
Luân Đôn – Bom–bay giảm: 17400 – 10100 = 7300 (km)
Mác–xây – Bom–bay giảm: 16000 – 7400 = 8600 (km)
Ô–đét–xa – Bom–bay giảm: 19000 – 6800 = 12200 (km).
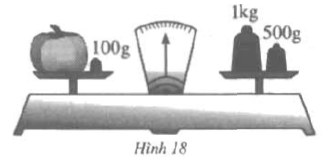
* Bài 43 trang 23 SGK Toán 6 Tập 1: Tính khối lượng của quả bí ở hình 18 khi cân thăng bằng:
 > Lời giải:
> Lời giải:
- Cân thăng bằng khi khối lượng ở 2 bên cân bằng nhau, tức là:
- Khối lượng bí + 100g = 1kg + 500g.
Đổi 1kg = 1000g.
- Như vậy ta có: khối lượng bí + 100g = 1000g + 500g
- khối lượng bí = 1000g + 500g – 100g = 1400g.
* Bài 44 trang 24 SGK Toán 6 Tập 1: Tìm số tự nhiên x, biết:
a) x : 13 = 41; b) 1428 : x = 14;
c) 4x : 17 = 0; d) 7x - 8 = 713;
e) 8(x - 3) = 0; f) 0 : x = 0
> Lời giải:
a) x : 13 =41
x = 41.13
x = 533.
b) 1428 : x = 14;
x = 1428 : 14
x = 102
c) 4x : 17 = 0
4x = 0.17
4x = 0
x = 0.
d) 7x – 8 = 713
7x = 713 + 8
7x = 721
x = 721 : 7
x = 103.
e) 8(x – 3) = 0
x – 3 = 0
x = 3.
f) 0 : x = 0.
* Bài 45 trang 24 SGK Toán 6 Tập 1: Điền vào ô trống sao cho a = b.q + r với 0 ≤ r < b.
| a | 392 | 278 | 357 | 420 | |
| b | 28 | 13 | 21 | 14 | |
| q | 25 | 12 | |||
| r | 10 | 0 |
> Lời giải:
Trong phép tính a = b.q + r thì a là số bị chia, b là số chia, q là thương, r là số dư. Vậy:
• Khi biết a và b, ta thực hiện phép chia a cho b để tìm thương q và số dư r.
• Khi biết b, q và r thì ta thực hiện phép tính b.q + r để tìm a (a = b.q + r).
• Khi biết a, q và r thì từ a = b.q + r suy ra b.q = a – r, suy ra b = (a – r):q.
- Thực hiện phép chia 392 cho 28 ta được : 392 = 28.14 + 0 nên q = 14 và r = 0.
- Thực hiện phép chia 278 cho 13 ta được: 278 = 13.21 + 5 nên q = 21 và r = 5.
- Thực hiện phép chia 357 cho 21 ta được: 357 = 21.17 + 0 nên q = 17 và r = 0.
b = 14, q = 25, r = 10 thì a = b.q + r =14.25 + 10 = 350 + 10 = 360.
a = 420, q = 12, r = 0 thì b = (a – r):q = 420:12 = 35.
Vậy ta có bảng sau khi điền như sau:
| a | 392 | 278 | 357 | 360 | 420 |
| b | 28 | 13 | 21 | 14 | 35 |
| q | 14 | 21 | 17 | 25 | 12 |
| r | 0 | 5 | 0 | 10 | 0 |
* Bài 46 trang 24 SGK Toán 6 Tập 1: a) Trong phép chia cho 2, số dư có thể bằng 0 hoặc bằng 1. Trong phép chia cho 3, cho 4, cho 5, số dư có thể bằng bao nhiêu?
b) Dạng tổng quát của số chia hết cho 2 là 2k, dạng tổng quát của số chia hết cho 2 dư 1 là 2k + 1 với k thuộc N. Hãy viết dạng tổng quát của số chia hết cho 3, chia cho 3 dư 1, số chia cho 3 dư 2.
> Lời giải:
a) Trong phép chia số tự nhiên a cho số tự nhiên b, số dư luôn phải nhỏ hơn số chia:
a = b.q + r, 0 ≤ r < b.
– Trong phép chia cho 3, số dư có thể bằng : 0, 1, 2
– Trong phép chia cho 4, số dư có thể bằng : 0, 1, 2, 3
– Trong phép chia cho 5, số dư có thể bằng : 0, 1, 2, 3, 4
b) Dạng tổng quát của số chia hết cho 3 là 3k (k ∈ N)
Dạng tổng quát của số chia cho 3 dư 1 là 3k + 1 (k ∈ N)
Dạng tổng quát của số chia cho 3 dư 2 là 3k + 2 (k ∈ N).
* Tổng quát: Dạng tổng quát của số chia cho m dư n là: m.k + n (k ∈ N).
Trên đây là bài viết vận dụng lý thuyết để giải một số Bài tập về phép trừ hai số tự nhiên, phép chia hết và phép chia có dư. Với một số dạng bài tập tiêu biểu như: Thực hiện phép trừ, phép chia hai số tự nhiên; Vận dụng tính chất các phép tính để tính nhanh; và tìm số chưa biết trong một đẳng thức (tìm x).. Hy vọng các em đã hiểu rõ hơn nội dung khối kiến thức này, chúc các em học tốt.
Đánh giá & nhận xét
- Tìm m để đường thẳng tiếp xúc với đường tròn Toán 10 - Hỏi nhanh đáp gọn
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của tam thức bậc 2
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa trị tuyệt đối
- Tìm giá trị nhỏ nhất (gtnn), giá trị lớn nhất (gtln) của biểu thức lớp 9
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa dấu căn
- Đơn vị Micro, Nano, Pico? Bảng mẫu đơn vị về ước số và bội số trong SI? Hỏi đáp môn Vật lí
- Hệ đơn vị SI là gì? 7 đơn vị cơ bản của hệ SI? Hỏi nhanh đáp gọn môn Vật lí
- Đặc điểm của Electron lớp ngoài cùng của nguyên tử là gì? Hỏi nhanh Hóa 10
- Cách viết cấu hình Electron nguyên tử lớp 10? Hỏi nhanh Hóa 10
- Quy tắc Hund và Nguyên lý bền vững lớp 10? Hỏi nhanh Hóa 10


































