Viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng - Hình học 10

21:22:5327/09/2021

Viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng cho trước cũng là một dạng toán về phương trình đường tròn mà chúng ta thường gặp.

Khối A (KhoiA) sẽ giới thiệu với các em cách viết viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng cho trước qua bài này một cách ngắn gọn, chi tiết và đẩy đủ để các em tham khảo.

I. Cách viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng

Giả sử đường tròn (C) có tâm I(a; b); bán kính R và và đường thẳng (d) cho trước

Viết phương trình tiếp tuyến của (C) vuông góc với đường thẳng (d):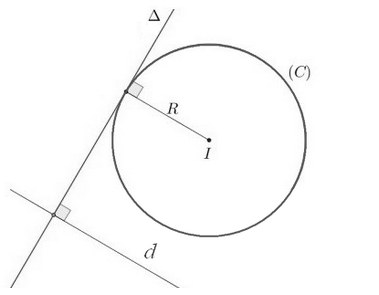 phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng Để viết phương trình tiếp tuyến Δ của đường tròn (C) vuông góc với đường thẳng (d): Ax + By + C = 0 ta thực hiện như sau:

- Bước 1: Xác định tâm I và bán kính R của đường tròn (C).

- Bước 2: Vì Δ ⊥ (d): Ax + By + C = 0 nên Δ có vectơ pháp tuyến là vectơ chỉ phương của (d): $\small \overrightarrow{n}_\Delta=\overrightarrow{u}_d=(B;-A)$

Khi đó phương trình tiếp tuyến Δ có dạng: Bx - Ay + c₁ = 0

- Bước 3: Vì Δ tiếp xúc với đường tròn (C) nên d(I,Δ) = R. Giải phương trình này ta tìm được c₁.

II. Bài tập vận dụng viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng

* Bài tập 1 (Bài 6 trang 84 SGK Hình học 10): Cho đường tròn C có phương trình: x² + y² – 4x + 8y – 5 = 0

Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng: 3x – 4y + 5 = 0.

> Lời giải:

- Ta có: x² + y² – 4x + 8y – 5 = 0

⇔ (x² – 4x + 4) + (y² + 8y + 16) = 25

⇔ (x – 2)² + (y + 4)² = 25.

Vậy (C) có tâm I(2 ; –4), bán kính R = 5.

- Gọi tiếp tuyến vuông góc với đường thẳng (d): 3x – 4y + 5 = 0 cần tìm là (Δ).

- Ta có (d) có VTPT $\small \overrightarrow{n}_d=(3;-4)\Rightarrow \overrightarrow{u}_d=(4;3)$

- Vì (Δ) ⊥ (d) nên có VTPT $\small \overrightarrow{n}_\Delta =\overrightarrow{u}_d=(4;3)$

Vậy phương trình tiếp tuyến (Δ) có dạng: 4x + 3y + c = 0.

$\small \Leftrightarrow \frac{|4.2+3(-4)+c|}{\sqrt{4^2+3^2}}=5 \Leftrightarrow \frac{|c-4|}{5}=5$

$\small \Leftrightarrow |c-4|=25\Leftrightarrow \left \[\begin{matrix} c-4=25\\ c-4=-25 \end{matrix} \right.$ $\small \Leftrightarrow \left \[\begin{matrix} c=29\\ c=-21 \end{matrix} \right.$

Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.

* Bài tập 2: Viết phương trình tiếp tuyến của đường tròn (C): x² + y² - 4x + 8y - 5 = 0. Biết tiếp tuyến vuông góc với đường thẳng (d); 3x + 4y + 21 = 0

> Lời giải:

- Ta có: x² + y² - 4x + 8y - 5 = 0

⇔ (x² - 4x + 4) + (y² + 2.4y + 16) - 25 = 0

⇔ (x - 2)² + (y + 4)² = 5²

Nên đường tròn (C) có tâm I(2;-4) và bán kính R = 5.

Tiếp tuyến Δ vuông góc với (d): 3x+ 4y + 21 = 0 nên Δ nhận VTCP của (d) làm VTPT, có:

$\small \overrightarrow{n}_d=(3;4)\Rightarrow \overrightarrow{u}_d=(4;-3) \Rightarrow \overrightarrow{n}_\Delta =(4;-3)$

Khi đó phương trình tiếp tuyến Δ có dạng: 4x - 3y + c = 0.

Vì Δ tiếp xúc với đường tròn (C) nên khoảng cách từ tâm I tới đường thẳng Δ bằng R: d(I,Δ) = R

$\small \Leftrightarrow \frac{|4.2-3.(-4)+c|}{\sqrt{(3^2)+(-4)^2}}=5 \Leftrightarrow \frac{|20+c|}{\sqrt{25}}=5$

$\small \Leftrightarrow |20+c|=25\Leftrightarrow \left \[\begin{matrix} 20+c=25\\ 20+c=-25 \end{matrix} \right.$ $\small \Leftrightarrow \left \[\begin{matrix} c=5\\ c=-45 \end{matrix} \right.$

Vậy có 2 tiếp tuyến thỏa yêu cầu là:

4x - 3y + 5 = 0 và 4x - 3y - 45 = 0.

Như vậy KhoiA.Vn đã giới thiệu với các em về cách viết về cách viết phương trình tiếp tuyến của đương tròn vuông góc với đường thẳng, hy vọng giúp các em hiểu bài hơn. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết nhé, chúc các em thành công.

Viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng - Hình học 10

Tags

Đánh giá & nhận xét