Tính chất của bất đẳng thức, Bất đẳng thức Cauchy (Cô- Si) và BĐT trị tuyệt đối - Toán lớp 10
Bất đẳng thức luôn là dạng luôn có nhiều bài toán khá khó, đây cũng không phải khái niệm xa lạ với các em khi chúng ta đã học kiến thức cơ bản về bất đẳng thức từ các lớp trước.
Trong nội dung bài này chúng ta sẽ hệ thống lại các tính chất của bất đẳng thức, đặc biệt về bất đẳng thức Cauchy (CÔ-SI) giữa trung bình cộng và trung bình nhân và bất đẳng thức trị tuyệt đối. Qua đó giải một số bài tập vận dụng để hiểu rõ nội dung lý thuyết bất đẳng thức.
I. Ôn tập về Bất đẳng thức
1. Khái niệm bất đẳng thức
- Các mệnh đề dạng "a<b" hoặc "a>b" được gọi là bất đẳng thức.
2. Bất đẳng thức hệ quả và bất đẳng thức tương đương
- Nếu mệnh đề "a<b ⇒ c<d" đúng thì ta nói bất đẳng thức c<d là bất đẳng thức hệ quả của bất đẳng thức a<b và cũng viết là a<b ⇒ c<d.
- Nếu bất đẳng thức a<b là hệ quả của bất đẳng thức c<d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là a<b ⇔ c<d.
3. Tính chất của bất đẳng thức
° Cộng hai vế của bất đẳng thức với một số:
a<b ⇔ a+c < b+c
° Nhân hai vế của bất đẳng thức với một số:
- Với c>0: a<b ⇔ ac < bc
- Với c<0: a<b ⇔ ac > bc
° Cộng hai bất đẳng thức cùng chiều
a<b và c<d ⇒ a+c < b+d
° Nhân hai bất đẳng thức cùng chiều
- Với a>0, c>0: a<b và c<d ⇒ ac < bd
° Nâng hai vế của bất đẳng thức lên một lũy thừa
- Với n ∈ N*: a<b ⇔ a2n+1 < b2n+1
- Với n ∈ N* và a>0: a<b ⇔ a2n < b2n
° Khai căn hai vế của một bất đẳng thức
- Với a>0: 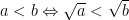
- Với a tùy ý: ![\dpi{100} a<b\Leftrightarrow \sqrt[3]{a}<\sqrt[3]{b}](http://khoia.vn/uploads/news/wyswyg/2020_12/160923036587s9mllbql.gif)
II. Bất đẳng thức Cauchy (Cô-Si) - Bất đẳng thức giữa trung bình cộng và trung bình nhân.
1. Bất đẳng thức Cauchy (Cô-si)
* Bất đẳng thức co-si với hai số không âm
- Cho a ≥ 0, b ≥ 0, ta có: 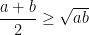
Dấu "=" xảy ra khi và chỉ khi a=b.
* Bất đẳng thức co-si với ba số không âm
- Cho a ≥ 0, b ≥ 0, c ≥ 0, ta có: ![\frac{a+b+c}{3}\geq \sqrt[3]{abc}](http://khoia.vn/uploads/news/wyswyg/2020_12/160923037988ykoqwtim.gif)
Dấu "=" xảy ra khi và chỉ khi a=b=c.
2. Các hệ quả của Bất đẳng thứ Cô-si
° Hệ quả 1: Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.
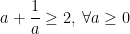
° Hệ quả 2: Nếu x, y cùng dương và có tổng không đổi thì tích xy lớn nhất khi và chỉ khi x=y.
→ Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
° Hệ quả 3: Nếu x, y cùng dương và có tích không đổi thì tổng x + y nhỏ nhất khi và chỉ khi x = y.
→ Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.
III. Bất đẳng thức chứa dấu trị tuyệt đối
Từ định nghĩa giá trị tuyệt đối, ta có tính chất bất đẳng thức trị tuyệt đối như sau
° |x| ≥ 0, |x| ≥ x, |x| ≥ -x
° Với a>0:
|x| ≤ 0 ⇔ -a ≤ x ≤ a
|x| ≥ a ⇔ x ≤ -a hoặc x ≥ a
° |a| - |b| ≤ |a + b| ≤ |a| + |b|
IV. Bài tập vận dụng Bất đẳng thức
* Bài 1 trang 79 SGK Đại Số 10: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x?
a) 8x > 4x ; b) 4x > 8x
c) 8x2 > 4x2 ; d) 8 + x > 4 + x
> Lời giải:
- Đáp án đúng: d) 8 + x > 4 + x
- Vì 8 > 4 nên với mọi x thì 8+ x > 4+ x ( tính chất cộng hai vế của BĐT với 1 số). Nên khẳng định d là đúng với mọi giá trị của x.
+ Các đáp án khác sai vì:
a) Ta có: 8 > 4 nên để 8x > 4x thì x > 0
- Do đó, chỉ đúng khi x > 0 (hay nói cách khác nếu x < 0 thì a sai)
b) Ta có: 4 < 8 nên để 4x > 8x thì x < 0 .
- Do đó, khẳng định chỉ đúng khi x < 0
c) chỉ đúng khi x ≠ 0
* Bài 2 trang 79 SGK Đại Số 10: Cho số x > 5, số nào trong các số sau đây là số nhỏ nhất?
A=5/x; B=5/x + 1; C = 5/x - 1; D = x/5.
> Lời giải:
- Với mọi x ≠ 0 ta luôn có: - 1 < 0 < 1. Do đó,
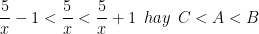
- Lại có x > 5 ⇒ x2 > 52 (Bình phương hai vế)
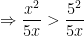 (nhân cả hai vế với 1/5x > 0)
(nhân cả hai vế với 1/5x > 0)
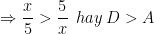
→ Vậy ta có C < A < B và C < A < D nên trong bốn số trên, C là số nhỏ nhất.
* Bài 3 trang 79 SGK Đại Số 10: Cho a, b, c là độ dài ba cạnh của một tam giác.
1) Chứng minh (b - c)2 < a2
2) Từ đó suy ra: a2 + b2 + c2 < 2(ab + bc + ca)
> Lời giải:
1) (b – c)2 < a2
- Vì a, b, c là độ dài 3 cạnh của một tam giác nên tổng 2 cạnh luôn lớn hơn cạnh còn lại. ⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
- Ta có: (b – c)2 - a2 = (b - c - a)(b - c + a)
Do b < a + c ⇒ b - a - c < 0 và b + a > c ⇒ b + a - c > 0.
Suy ra: (b - c - a)(b - c + a) < 0 ⇔ (b – c)2 - a2 < 0 ⇔ (b – c)2 < a2
2) Từ kết quả câu 1) ta có
a2 > (b - c)2
b2 > (a - c)2
c2 > (a - b)2
- Cộng vế với vế ba bất đẳng thức trên ta có:
a2 + b2 + c2 > (b – c)2 + (c – a)2 + (a – b)2
⇒ a2 + b2 + c2 > b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2
⇒ a2 + b2 + c2 > 2(a2 + b2 + c2) – 2(ab + bc + ca)
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).
* Bài 4 trang 79 SGK Đại Số 10: Chứng minh rằng: x3 + y3 ≥ x2y + xy2, ∀x, y ≥ 0
> Lời giải:
Với x ≥ 0; y ≥ 0 thì x + y ≥ 0
Ta có: x3 + y3 ≥ x2y + xy2
⇔ (x3 + y3) – (x2y + xy2) ≥ 0
⇔ (x + y)(x2 – xy + y2) – xy(x + y) ≥ 0
⇔ (x + y)(x2 – xy + y2 – xy) ≥ 0
⇔ (x + y)(x2 – 2xy + y2) ≥ 0
⇔ (x + y)(x – y)2 ≥ 0 (Luôn đúng vì x + y ≥ 0 ; (x – y)2 ≥ 0)
Dấu "=" xảy ra khi (x – y)2 = 0 ⇔ x = y.
* Bài 5 trang 79 SGK Đại Số 10: Chứng minh rằng:
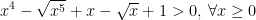
> Lời giải:
- Đặt t = √x (điều kiện t ≥ 0), khi đó:
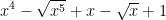
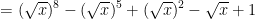
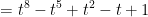
Ta cần chứng minh: 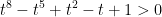
+ Xét 0 ≤ t < 1 ⇒ t3 < 1 ⇒ 1 – t3 > 0 ; 1 – t > 0
t8 – t5 + t2 – t + 1 = t8 + (t2 – t5) + (1 – t)
= t8 + t2.(1 – t3) + (1 – t) > 0 + 0 + 0 = 0
(vì t8 ≥ 0; t2 ≥ 0 ⇒ t2(1 - t3) ≥ 0)
+ Xét t ≥ 1 ⇒ t3 ≥ 1 ⇒ t3 – 1 ≥ 0 và t – 1 ≥ 0.
t8 – t5 + t2 – t + 1 = t5.(t3 – 1) + t.(t – 1) + 1 ≥ 0 + 0 + 1 > 0
Vậy với mọi t ≥ 0 thì t8 – t5 + t2 – t + 1 ≥ 1/2 > 0 hay
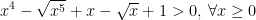
+ Cách giải khác:
2.(t8 – t5 + t2 – t + 1) = t8 + t8 – 2t5 + t2 + t2 – 2t + 1 + 1
= t8 + (t4 – t)2 + (t – 1)2 + 1 ≥ 0 + 0 + 0 + 1 = 1.
(Vì t8 ≥ 0 ; (t4 – t)2 ≥ 0; (t – 1)2 ≥ 0)
⇒ t8 – t5 + t2 – t + 1 ≥ 1/2 > 0 hay
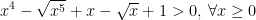
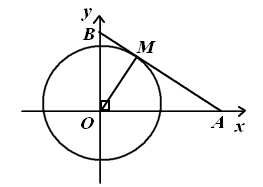
* Bài 6 trang 79 SGK Đại Số 10: Trong mặt phẳng tọa độ Oxy, trên các tia Ox và Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ của A và B để đoạn AB có độ dài nhỏ nhất.
 * Lời giải:
* Lời giải:
- Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).
Tóm lại, KhoiA hy vọng với bài viết hệ thống lại một số kiến thức về tính chất của bất đẳng thức, bất đẳng thức Cauchy (Cô-si) và bất đẳng thức trị tuyệt đối sẽ giúp các em hiểu rõ hơn thông qua các bài tập vận dụng.
Đánh giá & nhận xét
- Đơn vị Micro, Nano, Pico? Bảng mẫu đơn vị về ước số và bội số trong SI? Hỏi đáp môn Vật lí
- Hệ đơn vị SI là gì? 7 đơn vị cơ bản của hệ SI? Hỏi nhanh đáp gọn môn Vật lí
- Đặc điểm của Electron lớp ngoài cùng của nguyên tử là gì? Hỏi nhanh Hóa 10
- Cách viết cấu hình Electron nguyên tử lớp 10? Hỏi nhanh Hóa 10
- Quy tắc Hund và Nguyên lý bền vững lớp 10? Hỏi nhanh Hóa 10
- Nguyên lý Pauli và quy tắc Hund lớp 10? Hỏi nhanh Hóa 10
- Quy tắc Hund là gì? Tìm hiểu quy tắc Hund lớp 10, ví dụ về quy tắc Hund?
- Giải Vật lí 10 trang 92 Chân trời Sáng tạo
- Giải Vật lí 10 trang 91 Chân trời Sáng tạo
- Giải Vật lí 10 trang 90 Chân trời Sáng tạo


































