Toạ độ của một điểm và đồ thị của Hàm số? Toán 8 bài 2 Chân trời Tập 2 c5

Xác định Toạ độ của một điểm trong mặt phẳng toạ độ như nào, cách vẽ đồ thị của Hàm số ra sao? bài viết này sẽ cho các bạn lời giải đáp.

1. Toạ độ của một điểm

• Khái niệm Mặt phẳng toạ độ

Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.

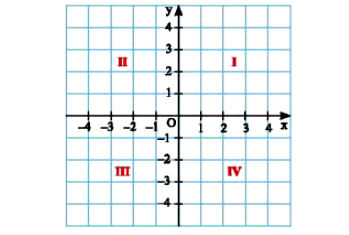
• Ox nằm ngang gọi là trục hoành;

• Oy thẳng đứng gọi là trục tung;

• O gọi là gốc tọa độ.

Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV.

• Toạ độ của một điểm trên Mặt phẳng toạ độ

Trong mặt phẳng tọa độ, mỗi điểm P xác định duy nhất một cặp số (a; b) và mỗi cặp số (a; b) xác định duy nhất một điểm P.

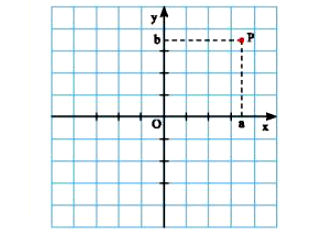
Cặp số (a; b) gọi là tọa độ của P, kí hiệu là P(a; b), trong đó a là hoành độ, b là tung độ của điểm P.

* Ví dụ: Điểm P có tọa độ là (1; –2), kí hiệu là P(1; –2). Số 1 gọi là hoành độ, số –2 gọi là tung độ của điểm P.

2. Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó

Để xác định một điểm điểm P có tọa độ là (a; b), ta thực hiện các bước sau:

• Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.

• Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.

• Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.

* Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.

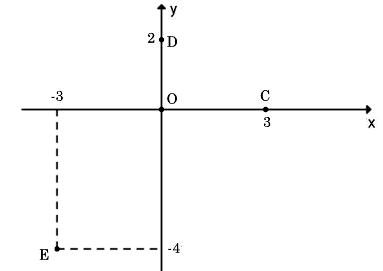
* Ví dụ: Vẽ một trục hệ tọa độ Oxy và đánh dấu các điểm C(3; 0), D(0; −2), E(−3; −4).

* Lời giải:

Các điểm C(3; 0), D(0; 2), E(−3; −4) được xác định trên mặt phẳng tọa độ Oxy như sau:

3. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).

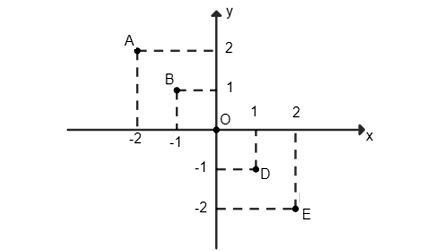
* Ví dụ: Vẽ đồ thị của hàm số y = f(x) cho bằng bảng sau:

Đồ thị hàm số là tập hợp các điểm có tọa độ A(−2; 2), B(−1; 1), O(0; 0), D(1; −1), E(2; −2) được vẽ trên mặt phẳng tọa độ sau: