Tìm m để hàm số nghịch biến trên khoảng, Hỏi nhanh đáp gọn môn Toán

Vậy cách tìm m để hàm số nghịch biến trên khoảng như thế nào? bài viết dưới đây sẽ giúp chúng ta có câu trả lời cụ thể.

• Hàm số nghịch biến khi nào?

Cho hàm số y = f(x) xác định trên K (với K là một khoảng hoặc một đoạn hoặc nửa khoảng).

- Hàm số y = f(x) là đồng biến (tăng) trên K nếu ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).

- Hàm số y = f(x) là nghịch biến (giảm) trên K nếu ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).

Hàm đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.

⇒ Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀x₁, x₂ ∈ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).

• Tìm m để hàm số nghịch biến trên khoảng

Ta thực hiện các bước sau:

+ Bước 1: Kiểm tra tập xác định: Vì bài toán có tham số nên ta cần tìm điều kiện của tham số để hàm số xác định trên khoảng (a;b).

+ Bước 2: Tính f'(x) và tìm điều kiện của tham số để f'(x) ≥ 0 hoặc f'(x) ≤ 0 trên khoảng (a;b) theo yêu cầu bài toán.

• Một số ví dụ: Tìm m để hàm số đồng biến trên khoảng

* Ví dụ 1: Tìm m để hàm số f(x) = –x³ + 3x² + 3mx – 1 nghịch biến trên khoảng (0; +∞)

* Lời giải:

- TXĐ: D = R

- Ta có: f'(x) = –3x² + 6x + 3m

- Để hàm số nghịch biến trên (0; +∞) thì f'(x) ≤ 0, ∀x ∈ (0; +∞).

 ⇒ –3x² + 6x + 3m ≤ 0,  ∀x ∈ (0; +∞).

⇒ m ≤ x² – 2x ,  ∀x ∈ (0; +∞).

- Đặt y(x) = x² – 2x ⇒ y' = 2x – 2

- Cho y' = 0 ⇒ x = 1. Ta có bảng biến thiên sau:

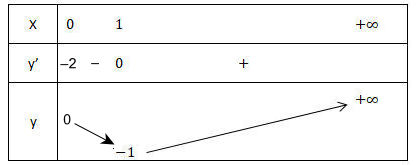
- Từ bảng biến thiên ta có: 

- Kết luận: Vậy với m ≤ –1 thì hàm số (*) nghịch biến trên khoảng (0;+∞).

* Ví dụ 2: Cho hàm số  . Tìm m để hàm số nghịch biến trên khoảng xác định của nó.

* Lời giải:

- TXĐ: D = R\{2}

Đạo hàm: 

Hàm số nghịch biến trên mỗi khoảng xác định của nó khi và chỉ khi y' ≤ 0, ∀x ∈ D.

(Dấu "=" chỉ xảy ra tại hữu hạn điểm trên D)

⇔ g(x) = –x² + 4x + 2m + 1 ≤ 0, ∀x ∈ D. 

Do hệ số của g(x) là: a = –1 < 0, nên g(x) ≤ 0 

⇔ Δ'_g ≤ 0 ⇔ 4 – (–1).(2m + 1) ≤ 0

⇔ 2m + 5 ≤ 0

⇔ m ≤ –5/2

Vậy hàm số nghịch biến trên khoảng xác định khi m m ≤ –5/2