Tìm m để đồ thị hàm số cắt trục hoành tại 3 điểm? Toán lớp 12 - Hỏi nhanh đáp gọn

Vậy cách Tìm m để đồ thị hàm số cắt trục hoành tại 3 điểm ra sao? đồ thị hàm số bậc 3 cắt trục hoành tại 3 điểm khi nào? Tất cả sẽ có lời giải đáp trong bài viết này để các bạn tham khảo.

1. Phương pháp giải bài toán tìm m để đồ thị hàm số cắt trục hoành Ox tại 3 điểm

Cho hàm số bậc 3: y = ax³ + bx² + cx + d với (a ≠ 0)

Để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt, chúng ta có thể giải theo một trong 2 cách sau tuỳ bài toán.

* Cách giải 1:

Viết phương trình hoành độ giao điểm, xác định số giao điểm của đồ thị hàm số y = f(x) với trục hoành Ox

Số giao điểm bằng số nghiệm của phương trình f(x) = 0

Nên để phương trình có 3 nghiệm thì ax³ + bx² + cx + d = 0 phải có 3 nghiệm phân biệt.

* Cách giải 2:

Để đồ thị hàm số cắt trục hoành tại 3 điểm thì: 

hay  (với x₁, x₂ là nghiệm của f'(x).

* Lưu ý: Cách giải 1 thường được dùng trong các bài toán nhẩm được nghiệm hoặc tách riêng được m và x; khi không nhẩm được nghiệm hay tác được m và x ta dùng cách 2.

2. Tìm m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt

Áp dụng phương pháp giải trên ta sẽ giải bài toán Tìm m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt qua ví dụ minh họa.

* Ví dụ 1: Cho hàm số bậc 3 sau: y = f(x) = x³ – 2mx² + (m + 2)x

Tìm m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

* Lời giải:

(Bài toán này ta dễ dàng nhận thấy x = 0 là nghiệm của f(x) = 0, nên ta giải phương trình hoành độ giao điểm)

Xét phương trình hoành độ giao điểm của hàm số đã cho và trục hoành Ox (y = 0):

x³ – 2mx² + (m + 2)x = 0

⇔ x(x² – 2mx + m + 2) = 0

⇔ x = 0 hoặc x² – 2mx + m + 2 (*)

Để đồ thị hàm số cắt trục hoành Ox tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt khác 0.

Kết luận: Với m ≠ –2, m < –1 hoặc m > 2 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

* Ví dụ 2: Cho hàm số bậc 3: y = f(x) = x³ – 12x + 1 – m

Tìm m để đồ thị hàm số cắt trục hoành Ox tại 3 điểm phân biệt.

* Lời giải:

(Bài toán này ta thấy f(x) = 0 dễ cô lập m nên đưa về dạng biện luận nghiệm của đồ thị)

Xét phương trình hoành độ giao điểm: 

x³ – 12x + 1 – m = 0 ⇔ x³ – 12x + 1 = m

Để đồ thị hàm số f(x) cắt trục hoành tại 3 điểm phân biệt thì đường thẳng y = m phải cắt đồ thị hàm số y = g(x) = x³ – 12x + 1 tại 3 điểm phân biệt.

Ta có g'(x) = 3x² – 12 = 0 ⇔ x = ±2

Ta có bảng biến thiên sau:

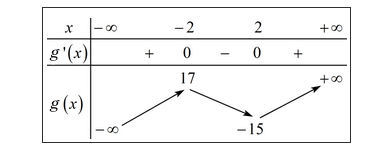
Dựa vào bảng biến thiên ta thấy để đường thẳng y = m cắt đồ thị hàm số y = g(x) tại 3 điểm phân biệt thì –15 < m < 17

Vây với –15 < m < 17 thì đồ thị hàm số bậc 3 đã cho cắt trục hoành tại 3 điểm phân biệt.

* Ví dụ 3: Cho hàm số bậc ba: y= f(x) = x³ – 3mx² + 3(m² – 1)x – m² + 1

Tìm m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

* Lời giải:

Ta có: f'(x) = 3x² – 6mx + 3(m² – 1) = 0

⇔ x = m – 1 hoặc x = m + 1

Suy ra: y_CD = (m – 1)³ – 3m(m – 1)² + 3(m² – 1)(m – 1) – m² + 1 = m³ – m² – 3m + 3

y_CT =  (m + 1)³ – 3m(m + 1)² + 3(m² – 1)(m + 1) – m² + 1 = m³ – m² – 3m – 1

Khi đó để hàm số cắt trục hoành tại 3 điểm phân biệt thì:

y_CT.y_CD < 0 ⇔ (m³ – m² – 3m + 3)(m³ – m² – 3m – 1) < 0

⇔ (m² – 1)(m² – 3)(m² – 2m – 1) < 0

 (*)

Vậy với m thoả (*) thì hàm số đã cho cắt trục hoành tại 3 điểm phân biệt.