Hàm số lũy thừa là gì? Cách tính đạo hàm của hàm số lũy thừa và khảo sát hàm số lũy thừa - Toán 12 bài 2
Hàm số lũy thừa là dạng hàm số có dạng y = xα với α là số thực cho trước. Đây là hàm số chúng ta cũng hay gặp trong các bài toán về khảo sát hàm số.
Cụ thể, hàm số lũy thừa là gì? cách tính đạo hàm của hàm số lũy thừa ra sao? Khảo sát hàm số lũy thừa như thế nào? chúng ta cùng tìm hiểu qua bài viết dưới đây nhé.
I. Khái niệm hàm số lũy thừa
• Hàm số lũy thừa là gì?
- Hàm số lũy thừa là các hàm số có dạng y = xα (với α ∈ R).
> Lưu ý:
- Các hàm số lũy thừa có tập xác định khác nhau, tùy theo α.
- Nếu α nguyên dương, tập xác định là R;
- Nếu α nguyên âm hoặc bằng 0, tập xác định là R\{0};
- Nếu α không nguyên, tập xác định là (0;+∞)
* Ví dụ: Hàm số: có tập xác định là [0;+∞)
Hàm số có tập xác định (0;+∞)
Hàm số có tập xác định R
Hàm số có tập xác định (0;+∞)
Như vậy, và
(hay
và
) là những hàm số khác nhau.
II. Đạo hàm của hàm số lũy thừa với số mũ tổng quát
• Hàm số y = xα có đạo hàm tại mọi x ∈ (0;+∞) và:
y' = (xα)'= α.xα-1
* Ví dụ: Tính đạo hàm của hàm: y = x3
> Lời giải:
- Áp dụng công thức (với α = 3) ta được: y' = (x3)' = 3x2.
• Nếu hàm số u = u(x) nhận giá trị dương và có đạo hàm trong khoảng J thì hàm số y = uα(x) cũng có đạo hàm trên J và:
y' = [u(xα)]'= α.uα-1(x).u'(x)
* Ví dụ: Tính đạo hàm của hàm: y = (x2 + 3x - 4)3
> Lời giải:
- Áp dụng công thức hàm hợp (với α = 3; u = x2 + 3x - 4), ta được:
y' = [(x2 + 3x - 4)3]' = 3.(x2 + 3x - 4)2.(2x + 3).
III. Khảo sát hàm số lũy thừa y = xα
Tương tự bài toán khảo sát hàm số đã học ở chương 1, khảo sát hàm số lũy thừa y=xα cũng tuân thủ đầy đủ các bước thực hiện sau:
- Bước 1: Tìm tập xác định (hay còn gọi là tập khảo sát).
- Bước 2: Xét sự biến thiên (biểu diễn bằng bảng biến thiên hàm số).
- Bước 3: Vẽ đồ thị hàm số đã cho (dựa vào bảng biến thiên bước 2).
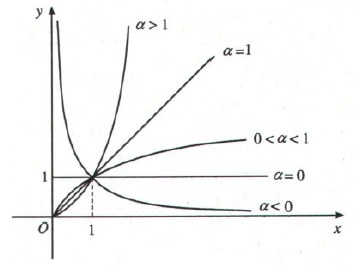 - Hình trên là đồ thị hàm số lũy thừa trên khoảng (0;+∞) ứng với các giá trị α khác nhau
- Hình trên là đồ thị hàm số lũy thừa trên khoảng (0;+∞) ứng với các giá trị α khác nhau
- Đồ thị của hàm số y = xα luôn đi qua điểm (1;1);
- Khi khảo sát hàm lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
IV. Câu hỏi vận dụng
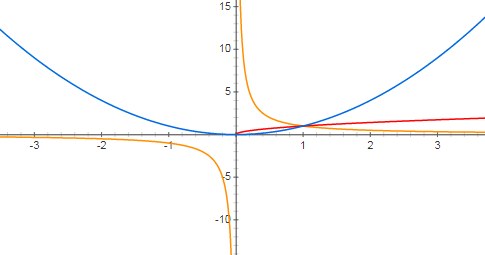
* Câu hỏi 1 trang 58 Toán 12 Giải tích: Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng: y = x2, y = x(1/2), y = x-1.
> Lời giải:
- Tập xác định của hàm số y = x2 là R.
- Tập xác định của hàm số y = x1/2 là [0,+∞).
- Tập xác định của hàm số y = x-1 là R\{0}.
Đồ thị của hàm số y = x2 đường màu xanh.
Đồ thị của hàm số y = x1/2 đường màu đỏ.
Đồ thị của hàm số y = x-1 đường màu cam.
* Câu hỏi 2 trang 58 Toán 12 Giải tích: Tính đạo hàm của các hàm số:
> Lời giải:
- Với ta có:
- Với ta có:
- Với ta có:
* Câu hỏi 3 trang 59 Toán 12 Giải tích: Tính đạo hàm của hàm số .
> Lời giải:
- Với ta có:
Trên đây KhoiA.Vn đã giới thiệu với các em về Hàm số lũy thừa, Cách tính đạo hàm của hàm số lũy thừa và khảo sát hàm số lũy thừa. Hy vọng bài viết giúp các em hiểu rõ hơn. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết, chúc các em thành công.
Đánh giá & nhận xét
- Giải Địa lí 12 trang 23 Chân trời Sáng tạo
- Giải Địa lí 12 trang 27 Chân trời Sáng tạo
- Giải Địa lí 12 trang 26 Chân trời Sáng tạo
- Giải Địa lí 12 trang 25 Chân trời Sáng tạo
- Giải Địa lí 12 trang 22 Chân trời Sáng tạo
- Giải Địa lí 12 trang 21 Chân trời Sáng tạo
- Giải Địa lí 12 trang 20 Chân trời Sáng tạo
- Giải Địa lí 12 trang 19 Chân trời Sáng tạo
- Giải Địa lí 12 trang 18 Chân trời Sáng tạo
- Giải Địa lí 12 trang 16 Chân trời Sáng tạo


































