Công thức lượng giác: Công thức cộng, Công thức nhân và Công thức Tổng và Tích - Đại số 10 chương 6 bài 3
Các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt (cung đối, cung bù, cung phụ,...), các em đã tìm hiểu ở bài học trước.
Bài viết này chúng ta sẽ tiếp tục tìm hiểu thêm các công thức lượng giác như: Công thức cộng lượng giác, Công thức nhân đôi, Công thức biến đổi tích thành tổng và công thức biến đổi tổng thành tích.
I. Công thức cộng lượng giác
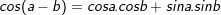
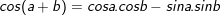
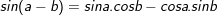
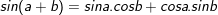
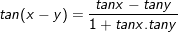
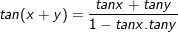
> Gợi ý cách ghi nhớ:
Cos thì cos cos sin sin
Sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi chàng
Sin thì giữ dấu xin nàng nhớ cho.
Tang tổng thì lấy tổng tang
Chia một trừ với tích tang, dễ òm.
II. Công thức nhân đôi
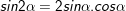
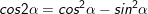
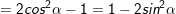
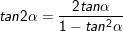
III. Công thức biến đổi tích thành tổng
![small cosa.cosb=frac{1}{2}left [ cos(a-b)+cos(a+b)
ight ]](http://khoia.vn/uploads/news/wyswyg/2021_03/1582900922uy2eo4f5os_1589789699_1615866235.gif)
![small sina.sinb=frac{1}{2}left [ cos(a-b)-cos(a+b)
ight ]](http://khoia.vn/uploads/news/wyswyg/2021_03/1582900946zatyswk9yq_1589789699_1615866235.gif)
![small sina.cosb=frac{1}{2}left [ sin(a-b)+sin(a+b)
ight ]](http://khoia.vn/uploads/news/wyswyg/2021_03/15829009477yny82pwy4_1589789700_1615866235.gif)
> Gợi ý cách ghi nhớ (theo thứ tự công thức):
Cos cos bằng nửa cos_trừ cộng cos_cộng
Sin sin bằng nửa cos_trừ trừ cos_cộng
Sin cos bằng nửa sin_trừ cộng sin_cộng
IV. Công thức biến đổi tổng thành tích
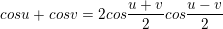
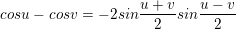
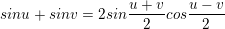
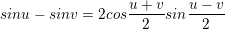
> Gợi ý cách ghi nhớ (theo thứ tự công thức):
cos cộng cos bằng hai cos cos
cos trừ cos bằng trừ hai sin sin
sin cộng sin bằng hai sin cos
sin trừ sin bằng hai cos sin
V. Bài tập vận dụng công thức lượng giác
* Bài 1 trang 153 SGK Đại số 10: Tính:
a) cos2250; sin2400; cot(-150); tan750
b) 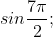
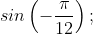
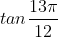
* Lời giải:
a) Ta có:
¤ 2250 = 1800 + 450 nên:
cos2250 = cos(1800 + 450) = -cos450 = (-√2)/2.
¤ sin2400 = sin(1800 + 600) = -sin600 = (-√3)/2.
¤ cot(-150) = -cot(150) = -cot(900 - 750) = -tan(750) = -tan(300 + 450)
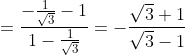
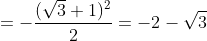
¤ tan750 = tan(900 - 150) = cot150 = -cot(-150) = -(-2-√3) = 2 + √3
- Nếu không tận dụng đáp án ý trước, ta có thể vận dụng công thức sau:
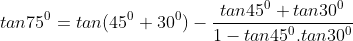
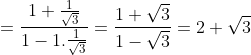
b) Ta có:
¤ 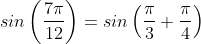
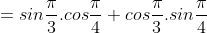
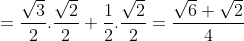
¤ 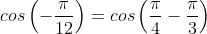
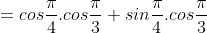
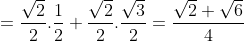
¤ 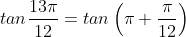
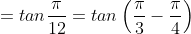
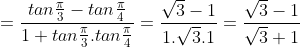
* Bài 2 trang 153 SGK Đại số 10: Tính:
a) 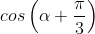 biết
biết 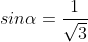 và
và 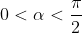
b) 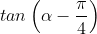 biết
biết 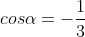 và
và 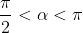
c) 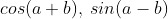 biết
biết 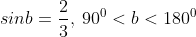
* Lời giải:
a) Ta có: 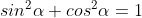
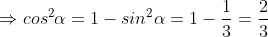
Vì 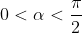 nên suy ra
nên suy ra 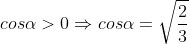
- Lại có: 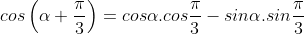
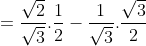
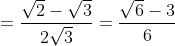
b) Ta có: 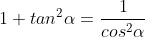
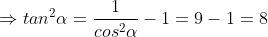
Mà 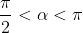 nên suy ra
nên suy ra 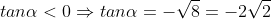
- Lai có: 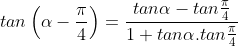
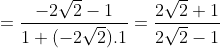
c) Ta có: 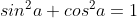
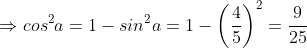
Mà 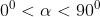 nên suy ra
nên suy ra 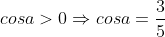
Tương tự: 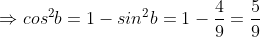
Mà 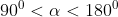 nên suy ra
nên suy ra 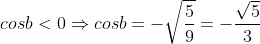
- Mặt khác, lại có:
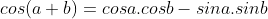
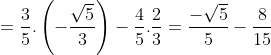
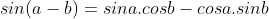
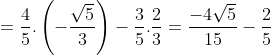
* Bài 6 trang 154 SGK Đại số 10: Cho: 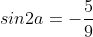 và
và 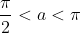 tính sina và cosa.
tính sina và cosa.
* Lời giải:
- Theo bài ra: 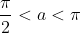 nên suy ra cosa<0 và sina>0.
nên suy ra cosa<0 và sina>0.
- Ta có: (sina - cosa)2 = sin2a + cos2a - 2.sina.cosa
= 1 - sin2a = 1 - (-5/9) = 14/9
Mà sina>0; cosa<0 nên sina - cosa>0 ⇒ sina - cosa = √14/9. (1)
- Lại có: (sina + cosa)2 = sin2a + cos2a + 2.sina.cosa
= 1 + sin2a = 1 + (-5/9) = 4/9
⇒ sina + cosa = 2/3 hoặc sina + cosa = -2/3.
¤ TH1: sina + cosa = 2/3. kết hợp với (1) ta được hệ pt:
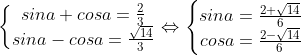
¤ TH2: sina + cosa = -2/3. kết hợp với (1) ta được hệ pt:
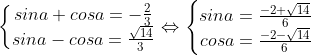
* Bài 7 trang 154 SGK Đại số 10: Biến đổi thành tích các biểu thức sau:
a) 1 – sinx; b) 1 + sinx;
c) 1 + 2cosx; d) 1 – 2sinx;
* Lời giải:
a) 1 – sinx;
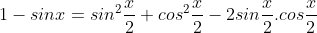
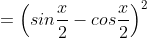
+) Cách khác: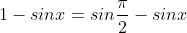
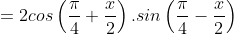
b) 1 + sinx;
- Biến đổi tươn tự câu a) ta có: 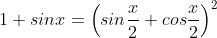
+) Cách khác: 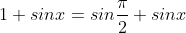
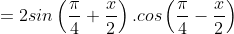
c) 1 + 2cosx
- Ta có: 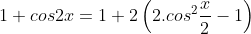
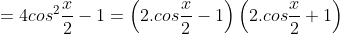
d) 1 – 2sinx
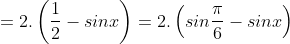
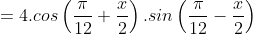
* Bài 8 trang 154 SGK Đại số 10: Rút gọn biểu thức:
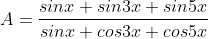
* Lời giải:
- Ta có: 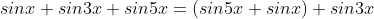
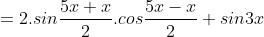
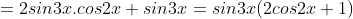
- Lại có: 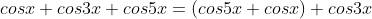
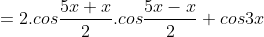
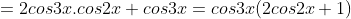
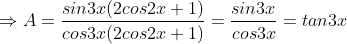
Tóm lại, bài viết là tập hợp các công thức cộng lượng giác, công thức nhân đôi, công thức biến đổi tích thành tổng và công thức biến đổi tổng thành tích mà các em phải ghi nhớ. Việc vận dụng các công thức này vào giải các bài tập sẽ giúp các em hiểu và ghi nhớ lâu hơn.
Đánh giá & nhận xét
- Đơn vị Micro, Nano, Pico? Bảng mẫu đơn vị về ước số và bội số trong SI? Hỏi đáp môn Vật lí
- Hệ đơn vị SI là gì? 7 đơn vị cơ bản của hệ SI? Hỏi nhanh đáp gọn môn Vật lí
- Đặc điểm của Electron lớp ngoài cùng của nguyên tử là gì? Hỏi nhanh Hóa 10
- Cách viết cấu hình Electron nguyên tử lớp 10? Hỏi nhanh Hóa 10
- Quy tắc Hund và Nguyên lý bền vững lớp 10? Hỏi nhanh Hóa 10
- Nguyên lý Pauli và quy tắc Hund lớp 10? Hỏi nhanh Hóa 10
- Quy tắc Hund là gì? Tìm hiểu quy tắc Hund lớp 10, ví dụ về quy tắc Hund?
- Giải Vật lí 10 trang 92 Chân trời Sáng tạo
- Giải Vật lí 10 trang 91 Chân trời Sáng tạo
- Giải Vật lí 10 trang 90 Chân trời Sáng tạo


































