Cách chứng minh 3 điểm thẳng hàng Toán lớp 10 (Vectơ tọa độ)

Bài viết này trình bày chi tiết cách chứng minh 3 điểm thẳng hàng Toán 10 (Vectơ tọa độ), nhằm giúp các em học sinh ôn tập, vận dụng chứng minh 3 điểm thẳng hàng dễ dàng.

1. Cách chứng minh 3 điểm thẳng hàng Toán 10 (Vectơ tọa độ)

• Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ  và  cùng phương. Hay A, B, C phân biệt thẳng hàng khi và chỉ khi tồn tại số thực k khác 0 sao cho: 

• Sử dụng các tính chất, quy tắc về phép toán vectơ,... để biến đổi đưa về điều cần chứng minh.

2. Cách chứng minh 3 điểm thẳng hàng Toán 10 qua ví dụ

* Ví dụ 1: Cho tam giác ABC có P là trung điểm của AB và M thuộc tia BC sao cho BC = CM, N thuộc cạnh AC sao cho AN = 2NC. Chứng minh rằng 3 điểm M, N, P thẳng hàng.

* Lời giải:

Ta có hình vẽ sau:

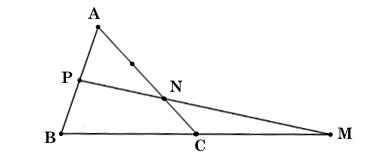
Vì M thuộc tia BC sao cho BC = CM nên  

Vì N thuộc cạnh AC sao cho AN = 2NC nên 

Vì P là trung điểm AB nên 

Theo quy tắc 3 điểm, ta có:  

 (1)

Lại có: 

 (2)

Từ (1) và (2) có: 

Vậy 3 điểm M, N, P thẳng hàng.

* Ví dụ 2: Cho hình bình hành ABCD. Gọi I là trung điểm của CD. Lấy điểm M trên đoạn BI sao cho BM = 2MI. Chứng minh A, M, C thẳng hàng.

* Lời giải:

Ta có hình vẽ sau:

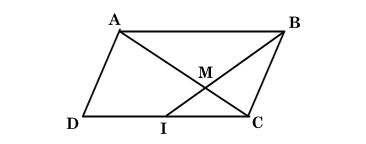Ta có: 

 (*)

Vì ABCD là hình bình hành nên

Mà I là trung điểm CD nên 

Thay vào đẳng thức (*) ở trên ta có:

Vậy ba điểm A, M, C thẳng hàng.

* Ví dụ 3: Trong mặt phẳng Oxy, cho ba điểm A(-1; 1), B(1; 3), C(3; 4)

Chứng minh ba điểm A, B, C thẳng hàng.

* Lời giải:

Ta có:  và 

Suy ra hai vectơ  cùng phương

Vì vậy, ba điểm A, B, C thẳng hàng.

* Ví dụ 4: Cho tam giác ABC, trung tuyến AD. Gọi M là trung điểm AD, điểm N thuộc AC sao cho . Chứng minh ba điểm B, M, N thẳng hàng.

* Lời giải:

Ta có hình vẽ sau:

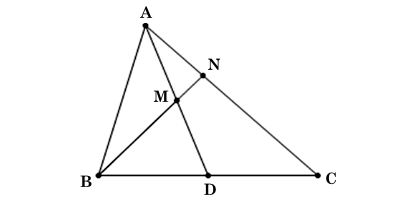
Ta có: 

Lại có:  (vì M là trung điểm của AD)

 (vì D là trung điểm của BC)

Vậy ba điểm B, M, N thẳng hàng.