Các công thức lượng giác lớp 10 cơ bản, tổng hợp đầy đủ - Toán 10 Đại số

14:06:4013/01/2021

Để giải được các bài toán về cung và góc lượng giác ở chương trình lớp 10, điều đầu tiên là các em phải nhớ được các công thức lượng giác cơ bản cũng như nâng cao.

Vì vậy bài viết này sẽ tổng hợp các công thức lượng giác cơ bản một cách đầy đủ nhất, thông qua đó giúp các em rèn luyện kỹ năng giải các bài toán về cung và góc lượng giác một cách chính xác nhất.

I. Công thức lượng giác 10: Giá trị lượng giác các cung đặc biệt

Giá trị lượng giác các cung đặc biệt

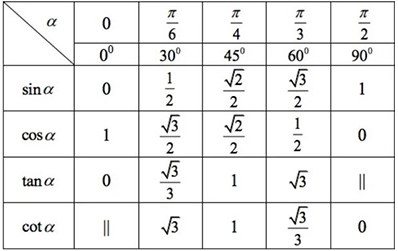
II. Công thức lượng giác 10: Các hệ thức cơ bản

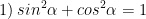
$1)\: sin^2\alpha +cos^2\alpha =1$

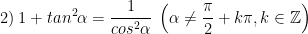
$2)\: 1+tan^2\alpha=\frac{1}{cos^2\alpha }\: \left ( \alpha \neq \frac{\pi }{2}+k\pi,k\in \mathbb{Z} \right )$

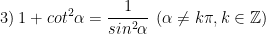
$3)\: 1+cot^2\alpha=\frac{1}{sin^2\alpha }\: \left ( \alpha \neq k\pi,k\in \mathbb{Z} \right )$

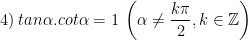
$4)\: tan\alpha .cot\alpha =1\: \left ( \alpha \neq \frac{k\pi }{2},k\in \mathbb{Z} \right )$

> Lưu ý: 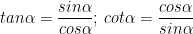$tan\alpha =\frac{sin\alpha }{cos\alpha };\: cot\alpha =\frac{cos\alpha }{sin\alpha }$

III. Công thức lượng giác 10: Các cung liên kết đặc biệt

Bao gồm công thức lượng giác 10 cho những cung, góc có mối liên hệ đặc biệt với nhau như: đối nhau, phụ nhau, bù nhau, hơn kém π, hơn kém π/2

1. Hai góc đối nhau (x và -x)

cos(–x) = cosx

sin(–x) = –sinx

tan(–x) = –tanx

cot(–x) = –cotx

2. Hai góc bù nhau (x và π - x)

sin(π - x) = sinx

cos(π - x) = -cosx

tan(π - x) = -tanx

cot(π - x) = -cotx

3. Hai góc hơn kém π (x và π + x)

sin(π + x) = -sinx

cos(π + x) = -cosx

tan(π + x) = tanx

cot(π + x) = cotx

4. Hai góc phụ nhau (x và π/2 - x)

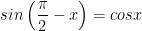
$sin\left ( \frac{\pi }{2}-x \right )=cosx$

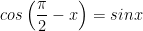
$cos\left ( \frac{\pi }{2}-x \right )=sinx$

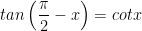
$tan\left ( \frac{\pi }{2}-x \right )=cotx$

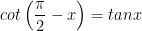
$cot\left ( \frac{\pi }{2}-x \right )=tanx$

5. Hai góc hơn kém nhau π/2 (x và π/2 + x)

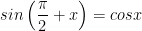
$sin\left ( \frac{\pi }{2}+x \right )=cosx$

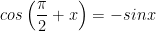
$cos\left ( \frac{\pi }{2}+x \right )=-sinx$

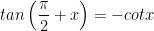
$tan\left ( \frac{\pi }{2}+x \right )=-cotx$

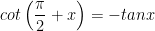
$cot\left ( \frac{\pi }{2}+x \right )=-tanx$

IV. Công thức lượng giác 10: Công thức cộng

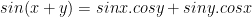
sin(x + y) = sinx.cosy + siny.cosx

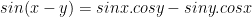
sin(x - y) = sinx.cosy - siny.cosx

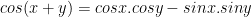
cos(x + y) = cosx.cosy - sinx.siny

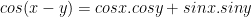
cos(x - y) = cosx.cosy + sinx.siny

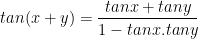
$tan(x+y)=\frac{tanx+tany}{1-tanx.tany}$

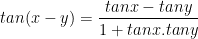
$tan(x-y)=\frac{tanx-tany}{1+tanx.tany}$

V. Công thức lượng giác 10: Công thức nhân đôi

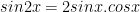
sin2x=2sinx.cosx

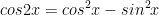
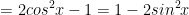
cos2x=cos^2x-sin^2x =2cos^2x-1=1-2sin^2x

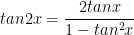
$tan2x=\frac{2tanx}{1-tan^2x}$

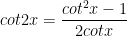
$cot2x=\frac{cot^2x-1}{2cotx}$

VI. Công thức lượng giác 10: Công thức nhân ba

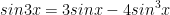
sin3x=3sinx-4sin^3x

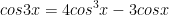
cos3x=4cos^3x-3cosx

VII. Công thức lượng giác 10: Công thức hạ bậc

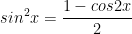
$sin^2x=\frac{1-cos2x}{2}$

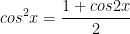
$cos^2x=\frac{1+cos2x}{2}$

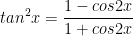
$tan^2x=\frac{1-cos2x}{1+cos2x}$

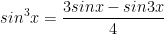
$sin^3x=\frac{3sinx-sin3x}{4}$

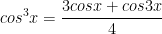
$cos^3x=\frac{3cosx+cos3x}{4}$

VIII. Công thức lượng giác 10: Công thức chia đôi

Để biểu diễn sinx, cosx và tanx theo t = tan(x/2)

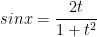
$sinx=\frac{2t}{1+t^2}$

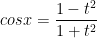
$cosx=\frac{1-t^2}{1+t^2}$

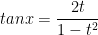
$tanx=\frac{2t}{1-t^2}$

IX. Công thức lượng giác 10: công thức tính tổng và hiệu sinx và cosx

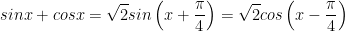
$sinx+cosx=\sqrt{2}sin\left ( x+\frac{\pi }{4} \right )=\sqrt{2}cos\left ( x-\frac{\pi }{4} \right )$

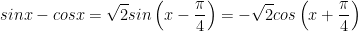
$sinx-cosx=\sqrt{2}sin\left ( x-\frac{\pi }{4} \right )=-\sqrt{2}cos\left ( x+\frac{\pi }{4} \right )$

X. Công thức lượng giác 10: Công thức biến đổi tổng thành tích

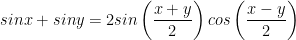
$sinx+siny=2sin\left ( \frac{x+y}{2} \right )cos\left ( \frac{x-y}{2} \right )$

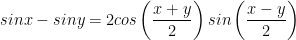
$sinx-siny=2cos\left ( \frac{x+y}{2} \right )sin\left ( \frac{x-y}{2} \right )$

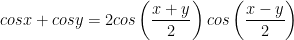
$cosx+cosy=2cos\left ( \frac{x+y}{2} \right )cos\left ( \frac{x-y}{2} \right )$

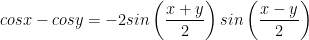
$cosx-cosy=-2sin\left ( \frac{x+y}{2} \right )sin\left ( \frac{x-y}{2} \right )$

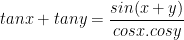
$\dpi{100} tanx+tany=\frac{sin(x+y)}{cosx.cosy}$

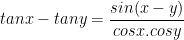
$tanx-tany=\frac{sin(x-y)}{cosx.cosy}$

XI. Công thức lượng giác 10: Công thức biến đổi tích thành tổng

$sinx.siny=\frac{1}{2}\left [ cos(x-y)-cos(x+y) \right ]$ $=-\frac{1}{2}[cos(x+y)-cos(x-y)]$

$cosx.cosy=\frac{1}{2}\left [ cos(x+y)+cos(x-y) \right ]$

$sinx.siny=\frac{1}{2}\left [ sin(x+y)+sin(x-y) \right ]$

Tóm lại, với bài viết tổng hợp đầy đủ các công thức lượng giác cơ bản và nâng cao ở trên, KhoiA tin rằng nếu các em nắm vững thì việc giải các bài toán lượng giác sẽ dễ dàng hơn rất nhiều.

Các em cần chú ý rằng, chúng ta cần giải các bài toán lượng giác vận dụng các công thức cơ bản trước để qua đó ghi nhớ công thức và từ từ hình thành kỹ năng giải toán và sẽ vận dụng tốt hơn các công thức nâng cao trong các bài toán phức tạp hơn.

Các công thức lượng giác lớp 10 cơ bản, tổng hợp đầy đủ - Toán 10 Đại số

Tags

Đánh giá & nhận xét