Bài 9.5 trang 86 Toán 11 Kết nối tri thức Tập 2

Bài 9.5 trang 86 Toán 11 Tập 2 Kết nối tri thức:

Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên L₁ và đoạn dốc xuống L₂ là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L₁ và L₂ phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc tọa độ đặt tại P và phương trình của parabol là y = ax² + bx + c, trong đó x tính bằng mét.

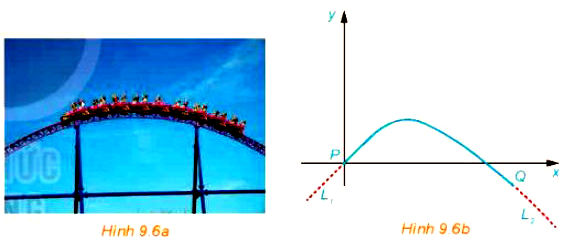
a) Tìm c.

b) Tính y'(0) và tìm b.

c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.

d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.

Giải bài 9.5 trang 86 Toán 11 Tập 2 Kết nối tri thức:

a) Tìm c.

Vì gốc tọa độ đặt tại P nên P(0; 0) nên ta có:

c = y(0) = 0.

Vậy c = 0.

b) Tính y'(0) và tìm b.

Ta tính được: y' = 2ax + b.

⇒ y'(0) = b.

Mà L₁ là phương trình tiếp tuyến tại P có hệ số góc 0,5 nên:

y'(0) = 0,5 ⇒ b = 0,5.

Vậy b = 0,5.

c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.

L₂ là phương trình tiếp tuyến tại Q có hệ số góc –0,75 nên

y'(x_Q) = 2ax_Q + 0,5 = –0,75.

Vì khoảng cách theo phương ngang giữa P và Q là 40 m nên:

x_Q – x_P = x_Q = 40.

⇒ 2a . 40 + 0,5 = –0,75

⇒ a = –1/64

Khi đó phương trình parabol là: 

d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.

Ta có: 

Vậy chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q là:

|y_P – y_Q| = 5.