Bài 8 trang 58 SGK Toán 7 tập 2 Chân trời sáng tạo

Bài 8 trang 58 SGK Toán 7 tập 2 Chân trời sáng tạo: Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:

a) AD = BC.

b) ΔEAB = ΔECD.

c) OE là tia phân giác của góc xOy.

Giải bài 8 trang 58 SGK Toán 7 tập 2 Chân trời sáng tạo:

Minh hoạ như hình vẽ sau:

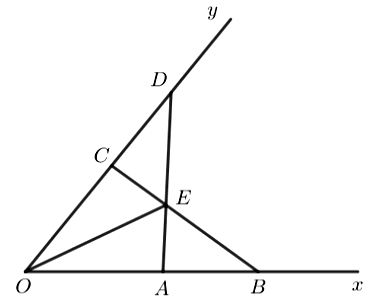
a) Xét hai tam giác OAD và OCB có:

OA = OC (theo giả thiết).

 chung.

OD = OB (theo giả thiết).

Do đó ΔOAD = ΔOCB (c-g-c).

⇒ AD = BC (2 cạnh tương ứng).

b) Do OA = OC, OB = OD

nên OB - OA = OD - OC hay AB = CD.

Do ΔOAD = ΔOCB (c-g-c) nên

  (2 góc tương ứng).

 là góc ngoài tại đỉnh C của tam giác OBC nên

  (1).

 là góc ngoài tại đỉnh A của tam giác OAD nên 

  (2).

Từ (1) và (2) suy ra 

Xét hai tam giác EAB và ECD có:

  (chứng minh trên).

AB = CD (chứng minh trên).

 (chứng minh trên).

Vậy nên: ΔEAB = ΔECD (g-c-g).

c) Do ΔEAB = ΔECD nên

 BE = DE (2 cạnh tương ứng).

Xét hai tam giác ODE và OBE có:

OD = OB (theo giả thiết).

OE chung.

DE = BE (theo giả thiết).

Do đó ΔODE = ΔOBE (c-c-c).

⇒  (2 góc tương ứng).

Vậy OE là tia phân giác của