Bài viết liên quan
Bài 6 trang 58 SGK Toán 7 tập 2 Chân trời sáng tạo
15:39:2915/03/2023
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:...
Bài 6 trang 58 SGK Toán 7 tập 2 Chân trời sáng tạo: Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) ΔEFH = ΔHGE.
b) EF // HG.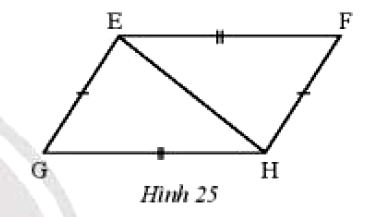
Giải bài 6 trang 58 SGK Toán 7 tập 2 Chân trời sáng tạo:
a) Xét hai tam giác EFH và HGE có:
EF = HG (theo giả thiết).
EG = HF (theo giả thiết).
cạnh EH chung.
Do đó ΔEFH = ΔHGE (c-c-c).
b) Vì ΔEFH = ΔHGE (c-c-c) nên
(2 góc tương ứng).
Mà hai góc này ở vị trí so le trong nên EF // HG.
Trên đây KhoiA.Vn đã hướng dẫn các em giải bài 6 trang 58 SGK Toán 7 Tập 2 Chân trời sáng tạo. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết nhé, chúc các em thành công.
• Xem hướng dẫn giải bài tập Trang 57,58 SGK Toán 7 Tập 2 Chân trời sáng tạo
Đánh giá & nhận xét
Bài viết khác
- Bài 9 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 8 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 7 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 6 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 5 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 4 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 3 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 2 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 1 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 9 trang 20 Toán 7 Chân trời sáng tạo Tập 2
Vật Lý
Xem tất cả
30/10/2024
Đơn vị Micro, Nano, Pico là một trong những đơn vị trong bảng mẫu đơn vị về ước số và bội số trong SI được sử dụng khá nhiều.
Hóa Học
Xem tất cả
03/10/2024
Đặc điểm của Electron lớp ngoài cùng của nguyên tử là gì? là thắc mắc của nhiều học sinh khi học môn Hóa học 10.
Tuyển sinh
Xem tất cả
03/05/2024
Đề minh họa môn Toán thi vào lớp 10 năm 2024 của Tp.Hà Nội được Sở GDĐT Hà Nội công bố để các thí sinh, quý thầy cô tham khảo.
A Cộng
Xem tất cả
09/09/2024
Nói quá, nói giảm, nói tránh là gì? Ví dụ nói quá, nói giảm nói tránh? là câu hỏi sẽ được giải đáp qua nội dung bài 7 SGK Ngữ văn lớp 7 chân trời sáng...
Hướng nghiệp
Xem tất cả




































