Bài 7.5 trang 36 Toán 11 Kết nối tri thức Tập 2

Bài 7.5 trang 36 Toán 11 Kết nối tri thức tập 2:

Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA ⊥ (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:

a) BC ⊥ (SAM)

b) Tam giác SBC cân tại S.

Giải bài 7.5 trang 36 Toán 11 Kết nối tri thức tập 2:

*Lưu ý: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Ta có hình vẽ sau:

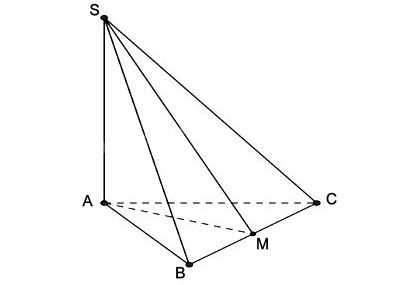
a) Chứng minh BC ⊥ (SAM)

Xét ΔABC cân tại A có

AM là đường trung tuyến (M là trung điểm BC)

⇒ AM là đường cao 

⇒ AM ⊥ BC   (1)

Lại có: SA ⊥ BC (vì SA ⊥ (ABC)) (2)

AM ∩ SA = {A}  (3)

Từ (1), (2) và (3) ⇒ BC ⊥ (SAM) (đpcm)

b) Chứng minh: Tam giác SBC cân tại S.

Theo câu a) ta có: BC ⊥ (SAM)

Mà SM ⊂ (SAM)

⇒ BC ⊥ SM

Xét ΔSBC có:

• SM là đường cao (vì BC ⊥ SM)

• SM là đường trung tuyến (M là trung điểm BC)

⇒ Tam giác SBC cân tại S (đpcm)