Bài 6 trang 36 Toán 12 Tập 1 Chân trời sáng tạo

Bài 6 trang 36 Toán 12 tập 1 Chân trời sáng tạo:

Bạn Việt muốn dùng tấm bia hình vuông cạnh 6 dm làm một chiếc hộp không nắp, có đáy là hình vuông bằng cách cắt bỏ đi 4 hình vuông nhỏ ở bốn góc của tấm bia (Hình 11).

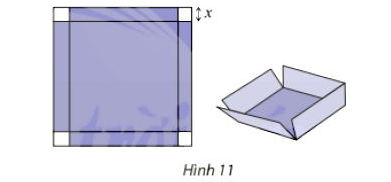
Bạn Việt muốn tìm độ dài cạnh hình vuông cần cắt bỏ để chiếc hộp đạt thể tích lớn nhất.

a) Hãy thiết lập hàm số biểu thị thể tích hộp theo x với x là độ dài cạnh hình vuông cần cắt đi.

b) Khảo sát và vẽ đồ thị hàm số tìm được

Từ đó, hãy tư vấn cho bạn Việt cách giải quyết vấn đề và giải thích vì sao cần chọn giá trị này. (Làm tròn kết quả đến hàng phần mười.)

Giải bài 6 trang 36 Toán 12 tập 1 Chân trời sáng tạo:

a) Chiều cao của hộp sau khi cắt là: x

Chiều dài của hộp sau khi cắt là: 6 – 2x

Chiều rộng của hộp sau khi cắt là: 6 – 2x

Vậy thể tích của hình hộp là: V(x) = x(6 - 2x)² = 4x³ - 24x² + 36x

b) Tập xác định: D = (0; 3)

Chiều biến thiên:

V'(x) = 12x² - 48x + 36 = 0 ⇔ x = 1 hoặc x = 3

Trên các khoảng (0; 1), (3; +∞) thì V'(x) > 0 nên hàm số đồng biến trên mỗi khoảng đó.

Trên khoảng (1; 3) thì V'(x) < 0 nên hàm số nghịch biến trên khoảng đó.

• Cực trị:

Hàm số đạt cực đại tại x = 1 và y_CĐ = 16

Hàm số đạt cực tiểu tại x = 3 và y_CT = 0

• Bảng biến thiên:

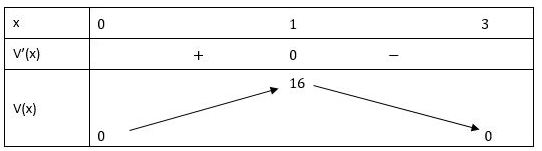
Khi x = 0 thì V(x) = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy

Ta có: V(x) = 0 ⇔ 4x³ - 24x² + 36x = 0 

⇔ x = 0 hoặc x = 3

Vậy đồ thị của hàm số giao với trục Ox tại điểm (0; 0) và (3; 0).

Đồ thị:

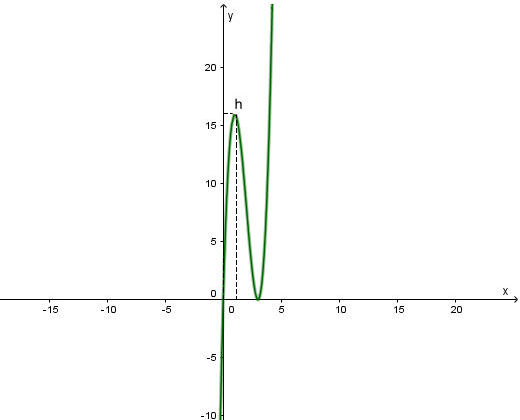Vì 0 < x < 3 (vì ở mỗi cạnh đều cắt đi 2 đầu nên nếu x ≥ 3 thì bạn Việt phải cắt hết tấm bìa. Do đó, bạn Việt nên cắt đi 4 hình vuông ở góc có cạnh bằng 1dm để thể tích của hộp đạt giá trị lớn nhất là 16dm³.