Bài 4 trang 78 SGK Toán 7 Tập 2 Chân trời sáng tạo
Cho tam giác nhọn ABC có ba đường cao AD, BE, CF....
Bài 4 trang 78 SGK Toán 7 tập 2 Chân trời sáng tạo: Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Giải bài 4 trang 78 SGK Toán 7 tập 2 Chân trời sáng tạo:
Ta có hình minh hoạ sau: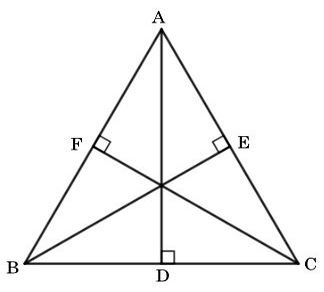
Xét ΔFBC vuông tại F và ΔECB vuông tại E có:
CF = BE (theo giả thiết).
cạnh BC chung.
⇒ ΔFBC = ΔECB (cạnh huyền - cạnh góc vuông).
(2 góc tương ứng).
+ Xét ΔABC có: nên ΔABC cân tại A.
Do đó AB = AC (1).
Xét ΔEAB vuông tại E và ΔDBA vuông tại D có:
BE = AD (theo giả thiết).
AB chung.
Do đó ΔEAB = ΔDBA (cạnh huyền - cạnh góc vuông).
(2 góc tương ứng).
+ Xét ΔABC có: nên ΔABC cân tại C.
Do đó CA = CB (2).
Từ (1) và (2) ta có:
AB = BC = CA ⇒ ΔABC đều.
Trên đây KhoiA.Vn đã hướng dẫn các em giải bài 4 trang 78 SGK Toán 7 Tập 2 Chân trời sáng tạo. Nếu có câu hỏi hay góp ý các em hãy để lại bình luận dưới bài viết nhé, chúc các em thành công.
• Xem hướng dẫn giải bài tập Trang 78 SGK Toán 7 Tập 2 Chân trời sáng tạo
Đánh giá & nhận xét
- Bài 9 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 8 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 7 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 6 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 5 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 4 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 3 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 2 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 1 trang 23 Toán 7 Chân trời sáng tạo Tập 2
- Bài 9 trang 20 Toán 7 Chân trời sáng tạo Tập 2




































