Bài 9.7 trang 90 Toán 8 Kết nối tri thức Tập 2

Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức:

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA′B′C′ ∽ ΔABC.

Chứng minh rằng: 

Giải Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức:

Ta có hình vẽ sau:

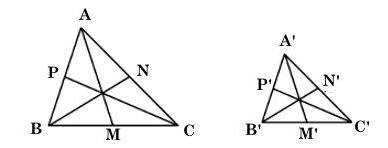
Vì ΔA′B′C′ ∽ ΔABC nên:  (1)

Và ; ;  (2)

Xét tam giác A'B'M' và ABM có:

 (theo (1))

 (theo (2))

Nên  ΔA′M′B′ ∽ ΔAMB (c.g.c)

 (3)

Tương tự, có ΔA′C′P′ ∽ ΔACP 

 (4)

Và ΔA′B′N′ ∽ ΔABN

 (5)

Từ (1), (3), (4) và (5) ta có: