Bài 9.13 trang 92 Toán 8 Kết nối tri thức Tập 2

Bài 9.13 trang 92 Toán 8 Tập 2 Kết nối tri thức:

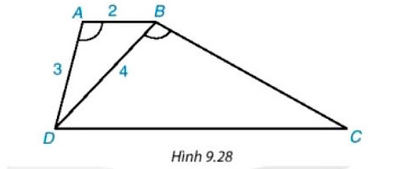
Cho hình thang ABCD (AB // CD) có ∠DAB = ∠DBC (hình 9.28)

a) Chứng minh rằng ΔABD ∽ ΔBDC. 

b) Giả sử AB = 2 cm, AD = 3 cm, BD = 4 cm. Tính độ dài các cạnh BC và DC.

Giải bài 9.13 trang 92 Toán 8 Tập 2 Kết nối tri thức:

a) Vì AB // CD (giả thiết) nên

 (2 góc ở vị trí so le trong).

Xét ΔABD và ΔBDC có:

 (chứng minh trên)

 (giả thiết)

⇒ ΔABD ∽ ΔBDC (g.g).

b) Ta có:

Vậy ΔABD ∽ ΔBDC với tỉ số đồng dạng 1/2.

 hay 

⇒ BC = 2 . 3 = 6 cm; DC = 4 . 2 = 8 cm.