Bài 7.13 trang 43 Toán 11 Kết nối tri thức Tập 2

Bài 7.13 trang 43 Toán 11 Kết nối tri thức Tập 2:

Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi đểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng:

a) Hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau;

b) Đường xiên SM lớn hơn đường xiên SM' nếu hình chiếu HM lớn hơn hình chiếu HM'.

Giải bài 7.13 trang 43 Toán 11 Kết nối tri thức Tập 2:

Ta có hình vẽ sau:

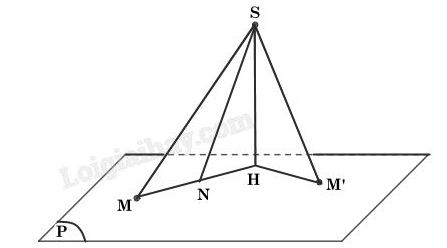
a) Có H là hình chiếu của S trên mặt phẳng (P) nên SH ⊥ (P),

⇒ SH ⊥ HM, SH ⊥ HM'.

- Giả sử SM = SM'.

Xét tam giác SHM vuông tại H, có SM² = SH² + HM²

Xét tam giác SHM' vuông tại H, có SM'² = SH² + HM'².

Mà SM = SM' nên HM = HM'.

- Giả sử HM = HM'.

Xét tam giác SHM vuông tại H, có SM² = SH² + HM²

Xét tam giác SHM' vuông tại H, có SM'² = SH² + HM'².

Mà HM = HM' nên SM = SM'.

Vậy hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau.

b) Trên tia HM lấy điểm N sao cho SN = SM' suy ra HN = HM'.

Mà SM > SM' nên SM > SN

⇒ HM > HN hay HM > HM'.