Bài 4 trang 56 SGK Toán 10 tập 1 Chân trời sáng tạo

Bài 4 trang 56 SGK Toán 10 tập 1 Chân trời sáng tạo: Cho hàm số bậc hai y = f(x) = ax² + bx + c có f(0) = 1, f(1) = 2, f(2) = 5.

a) Hãy xác định giá trị của các hệ số a, b, c.

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

Giải bài 4 trang 56 SGK Toán 10 tập 1 Chân trời sáng tạo: 

Theo bài ra, ta có:

f(0) = a.0² + b.0 + c = 1 ⇔ c = 1.

f(1) = a.1² + b.1 + c = 2 ⇔  a + b + c = 2.

f(2) = a.2² + b.2 + c = 5 ⇔  4a + 2b + c = 5.

Khi đó, ta có hệ phương trình: 

Vậy a = 1, b = 0 và c = 1.

Khi đó hàm số bậc 2 có dạng: y = f(x) = x² + 1

b) Với a = 1, b = 0 và c = 1 thì ta có hàm số: y = x² + 1.

Xét hàm số bậc hai: y = x² + 1, có:

Đỉnh S có tọa độ x_s = -b/2a = -0/2.1 = 0.

Suy ra: y_s = 0² + 1 = 1.

Hay S(0; 1).

Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:

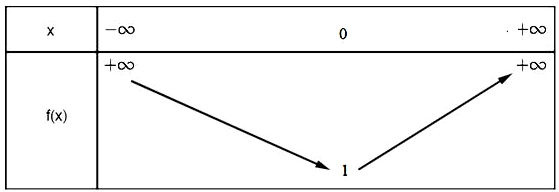
Dựa vào bảng biến thiên ta thấy:

Hàm số có giá trị nhỏ nhất bằng 1 khi x = 0. Do đó tập giá trị của hàm số là [1; +∞).

Hàm số nghịch biến trên khoảng (-∞;0) và đồng biến trên khoảng (0; +∞).